Conformal PID Control for Time Series Prediction

We study the problem of uncertainty quantification for time series prediction, with the goal of providing easy-to-use algorithms with formal guarantees. The algorithms we present build upon ideas from conformal prediction and control theory, are able to prospectively model conformal scores in an online setting, and adapt to the presence of systematic errors due to seasonality, trends, and general distribution shifts. Our theory both simplifies and strengthens existing analyses in online conformal prediction. Experiments on 4-week-ahead forecasting of statewide COVID-19 death counts in the U.S. show an improvement in coverage over the ensemble forecaster used in official CDC communications. We also run experiments on predicting electricity demand, market returns, and temperature using autoregressive, Theta, Prophet, and Transformer models. We provide an extendable codebase for testing our methods and for the integration of new algorithms, data sets, and forecasting rules.

The phase transition for the existence of the maximum likelihood estimate in high-dimensional logistic regression

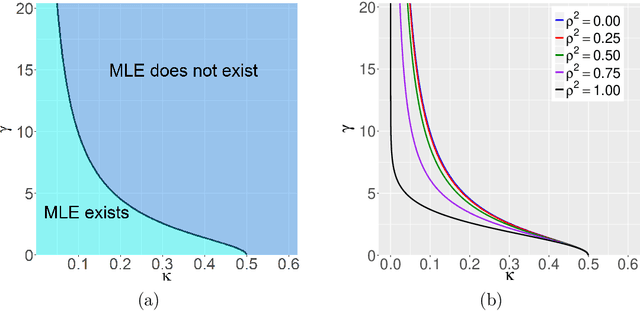
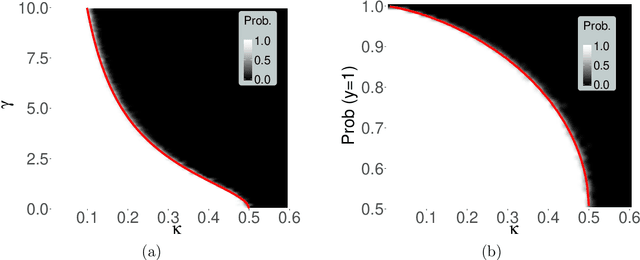
This paper rigorously establishes that the existence of the maximum likelihood estimate (MLE) in high-dimensional logistic regression models with Gaussian covariates undergoes a sharp `phase transition'. We introduce an explicit boundary curve $h_{\text{MLE}}$, parameterized by two scalars measuring the overall magnitude of the unknown sequence of regression coefficients, with the following property: in the limit of large sample sizes $n$ and number of features $p$ proportioned in such a way that $p/n \rightarrow \kappa$, we show that if the problem is sufficiently high dimensional in the sense that $\kappa > h_{\text{MLE}}$, then the MLE does not exist with probability one. Conversely, if $\kappa < h_{\text{MLE}}$, the MLE asymptotically exists with probability one.

Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems

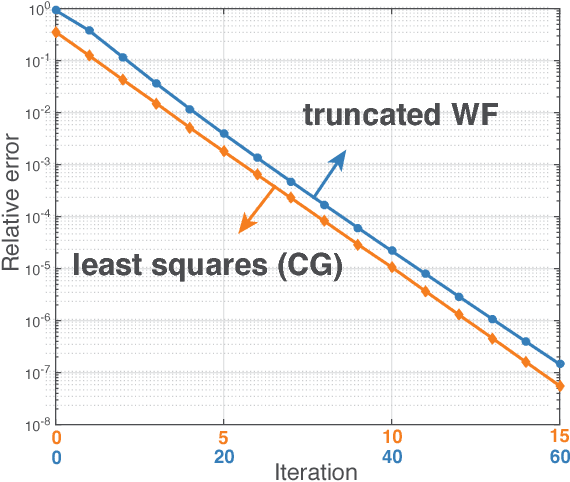
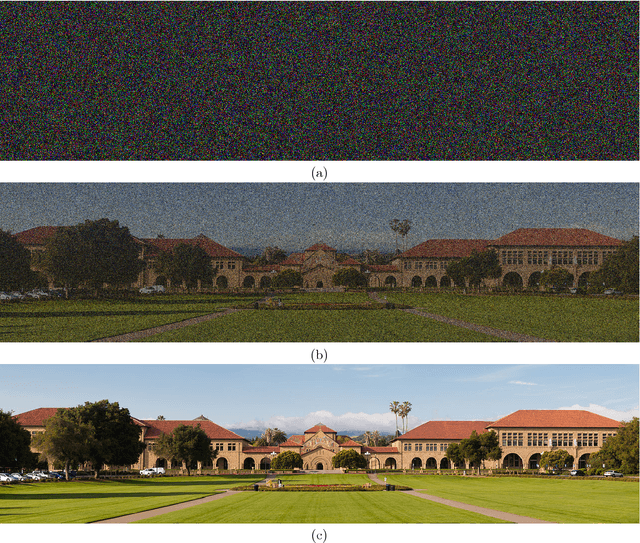
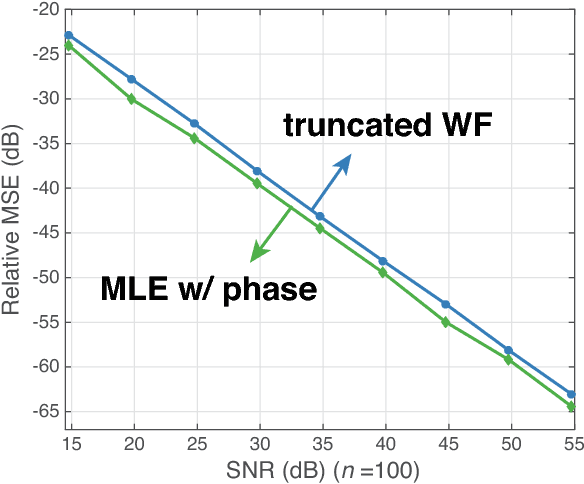
We consider the fundamental problem of solving quadratic systems of equations in $n$ variables, where $y_i = |\langle \boldsymbol{a}_i, \boldsymbol{x} \rangle|^2$, $i = 1, \ldots, m$ and $\boldsymbol{x} \in \mathbb{R}^n$ is unknown. We propose a novel method, which starting with an initial guess computed by means of a spectral method, proceeds by minimizing a nonconvex functional as in the Wirtinger flow approach. There are several key distinguishing features, most notably, a distinct objective functional and novel update rules, which operate in an adaptive fashion and drop terms bearing too much influence on the search direction. These careful selection rules provide a tighter initial guess, better descent directions, and thus enhanced practical performance. On the theoretical side, we prove that for certain unstructured models of quadratic systems, our algorithms return the correct solution in linear time, i.e. in time proportional to reading the data $\{\boldsymbol{a}_i\}$ and $\{y_i\}$ as soon as the ratio $m/n$ between the number of equations and unknowns exceeds a fixed numerical constant. We extend the theory to deal with noisy systems in which we only have $y_i \approx |\langle \boldsymbol{a}_i, \boldsymbol{x} \rangle|^2$ and prove that our algorithms achieve a statistical accuracy, which is nearly un-improvable. We complement our theoretical study with numerical examples showing that solving random quadratic systems is both computationally and statistically not much harder than solving linear systems of the same size---hence the title of this paper. For instance, we demonstrate empirically that the computational cost of our algorithm is about four times that of solving a least-squares problem of the same size.

A Differential Equation for Modeling Nesterov's Accelerated Gradient Method: Theory and Insights

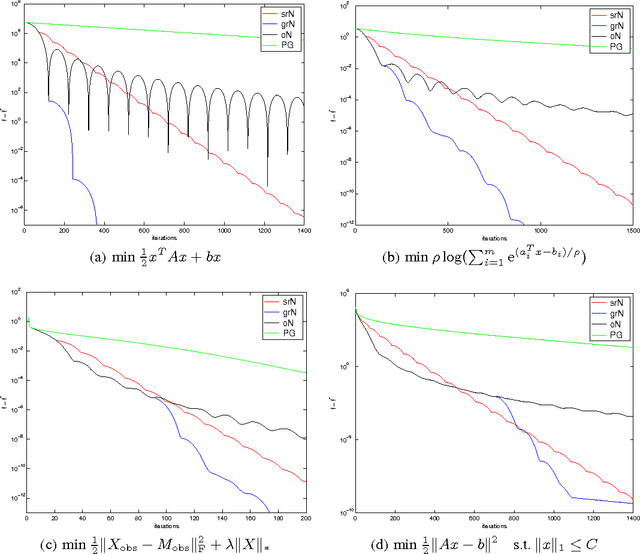
We derive a second-order ordinary differential equation (ODE) which is the limit of Nesterov's accelerated gradient method. This ODE exhibits approximate equivalence to Nesterov's scheme and thus can serve as a tool for analysis. We show that the continuous time ODE allows for a better understanding of Nesterov's scheme. As a byproduct, we obtain a family of schemes with similar convergence rates. The ODE interpretation also suggests restarting Nesterov's scheme leading to an algorithm, which can be rigorously proven to converge at a linear rate whenever the objective is strongly convex.