Solving Random Quadratic Systems of Equations Is Nearly as Easy as Solving Linear Systems
Paper and Code
Mar 22, 2016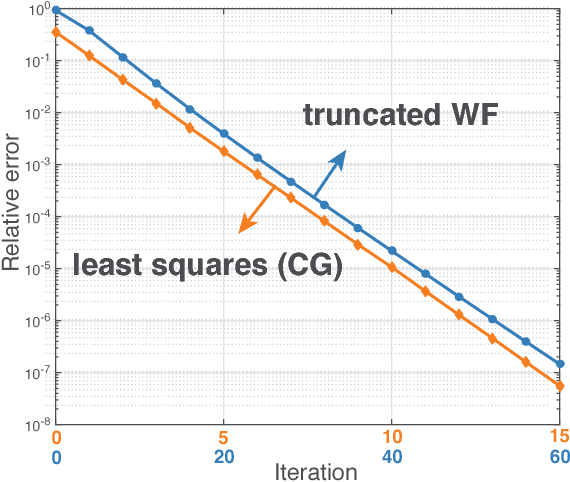
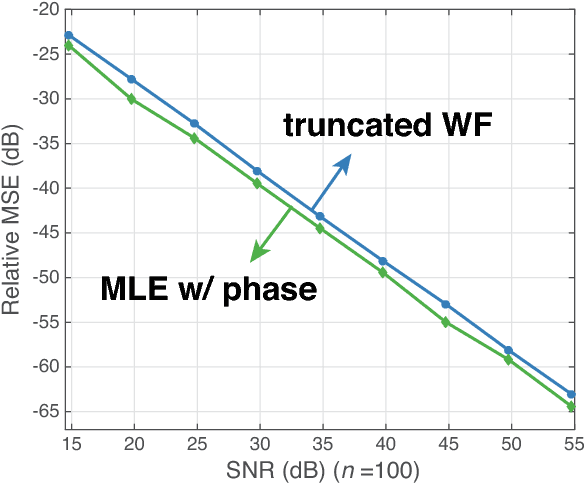
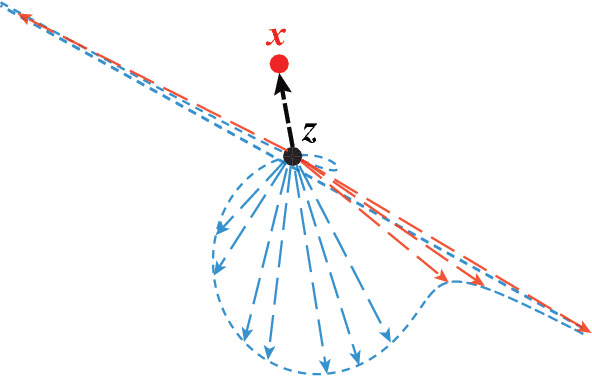
We consider the fundamental problem of solving quadratic systems of equations in $n$ variables, where $y_i = |\langle \boldsymbol{a}_i, \boldsymbol{x} \rangle|^2$, $i = 1, \ldots, m$ and $\boldsymbol{x} \in \mathbb{R}^n$ is unknown. We propose a novel method, which starting with an initial guess computed by means of a spectral method, proceeds by minimizing a nonconvex functional as in the Wirtinger flow approach. There are several key distinguishing features, most notably, a distinct objective functional and novel update rules, which operate in an adaptive fashion and drop terms bearing too much influence on the search direction. These careful selection rules provide a tighter initial guess, better descent directions, and thus enhanced practical performance. On the theoretical side, we prove that for certain unstructured models of quadratic systems, our algorithms return the correct solution in linear time, i.e. in time proportional to reading the data $\{\boldsymbol{a}_i\}$ and $\{y_i\}$ as soon as the ratio $m/n$ between the number of equations and unknowns exceeds a fixed numerical constant. We extend the theory to deal with noisy systems in which we only have $y_i \approx |\langle \boldsymbol{a}_i, \boldsymbol{x} \rangle|^2$ and prove that our algorithms achieve a statistical accuracy, which is nearly un-improvable. We complement our theoretical study with numerical examples showing that solving random quadratic systems is both computationally and statistically not much harder than solving linear systems of the same size---hence the title of this paper. For instance, we demonstrate empirically that the computational cost of our algorithm is about four times that of solving a least-squares problem of the same size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge