The phase transition for the existence of the maximum likelihood estimate in high-dimensional logistic regression
Paper and Code
Apr 25, 2018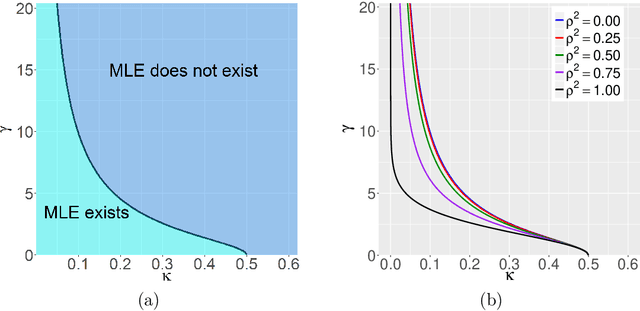
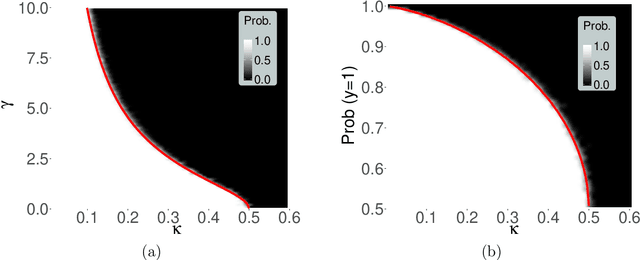
This paper rigorously establishes that the existence of the maximum likelihood estimate (MLE) in high-dimensional logistic regression models with Gaussian covariates undergoes a sharp `phase transition'. We introduce an explicit boundary curve $h_{\text{MLE}}$, parameterized by two scalars measuring the overall magnitude of the unknown sequence of regression coefficients, with the following property: in the limit of large sample sizes $n$ and number of features $p$ proportioned in such a way that $p/n \rightarrow \kappa$, we show that if the problem is sufficiently high dimensional in the sense that $\kappa > h_{\text{MLE}}$, then the MLE does not exist with probability one. Conversely, if $\kappa < h_{\text{MLE}}$, the MLE asymptotically exists with probability one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge