Minimum complexity interpolation in random features models
Paper and Code
Mar 30, 2021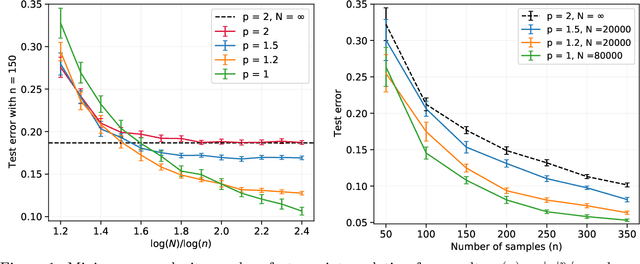
Despite their many appealing properties, kernel methods are heavily affected by the curse of dimensionality. For instance, in the case of inner product kernels in $\mathbb{R}^d$, the Reproducing Kernel Hilbert Space (RKHS) norm is often very large for functions that depend strongly on a small subset of directions (ridge functions). Correspondingly, such functions are difficult to learn using kernel methods. This observation has motivated the study of generalizations of kernel methods, whereby the RKHS norm -- which is equivalent to a weighted $\ell_2$ norm -- is replaced by a weighted functional $\ell_p$ norm, which we refer to as $\mathcal{F}_p$ norm. Unfortunately, tractability of these approaches is unclear. The kernel trick is not available and minimizing these norms requires to solve an infinite-dimensional convex problem. We study random features approximations to these norms and show that, for $p>1$, the number of random features required to approximate the original learning problem is upper bounded by a polynomial in the sample size. Hence, learning with $\mathcal{F}_p$ norms is tractable in these cases. We introduce a proof technique based on uniform concentration in the dual, which can be of broader interest in the study of overparametrized models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge