Time-varying Gaussian Process Bandit Optimization with Non-constant Evaluation Time

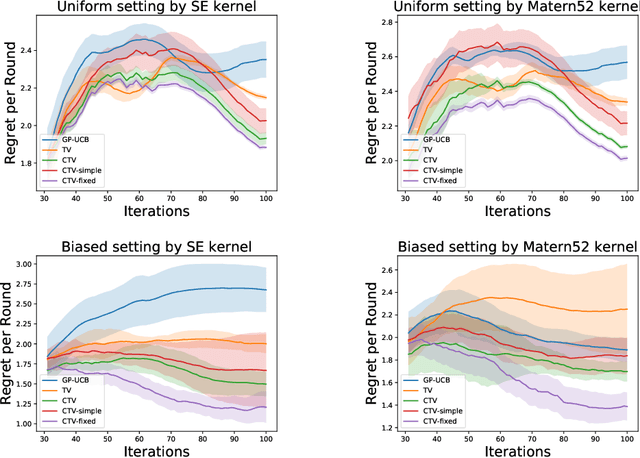
The Gaussian process bandit is a problem in which we want to find a maximizer of a black-box function with the minimum number of function evaluations. If the black-box function varies with time, then time-varying Bayesian optimization is a promising framework. However, a drawback with current methods is in the assumption that the evaluation time for every observation is constant, which can be unrealistic for many practical applications, e.g., recommender systems and environmental monitoring. As a result, the performance of current methods can be degraded when this assumption is violated. To cope with this problem, we propose a novel time-varying Bayesian optimization algorithm that can effectively handle the non-constant evaluation time. Furthermore, we theoretically establish a regret bound of our algorithm. Our bound elucidates that a pattern of the evaluation time sequence can hugely affect the difficulty of the problem. We also provide experimental results to validate the practical effectiveness of the proposed method.

Analysis of Minimax Error Rate for Crowdsourcing and Its Application to Worker Clustering Model

While crowdsourcing has become an important means to label data, there is great interest in estimating the ground truth from unreliable labels produced by crowdworkers. The Dawid and Skene (DS) model is one of the most well-known models in the study of crowdsourcing. Despite its practical popularity, theoretical error analysis for the DS model has been conducted only under restrictive assumptions on class priors, confusion matrices, or the number of labels each worker provides. In this paper, we derive a minimax error rate under more practical setting for a broader class of crowdsourcing models including the DS model as a special case. We further propose the worker clustering model, which is more practical than the DS model under real crowdsourcing settings. The wide applicability of our theoretical analysis allows us to immediately investigate the behavior of this proposed model, which can not be analyzed by existing studies. Experimental results showed that there is a strong similarity between the lower bound of the minimax error rate derived by our theoretical analysis and the empirical error of the estimated value.