Implicit Regularization with Polynomial Growth in Deep Tensor Factorization
Paper and Code
Jul 18, 2022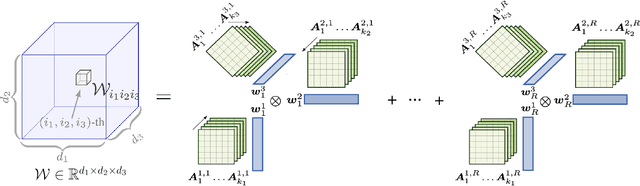
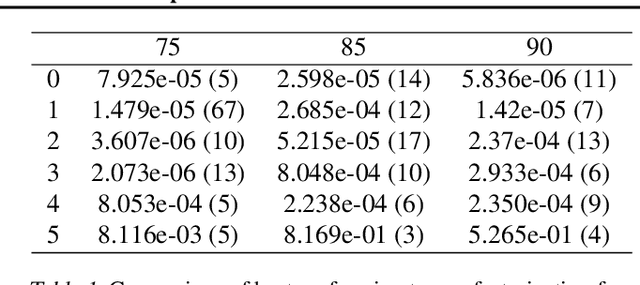
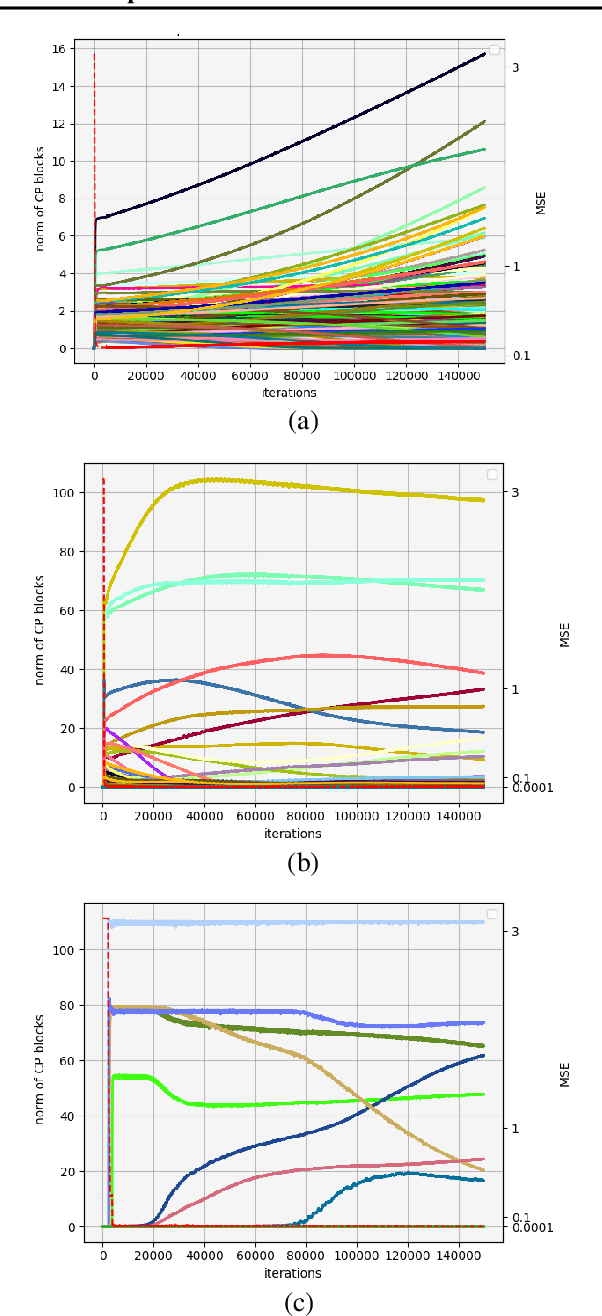
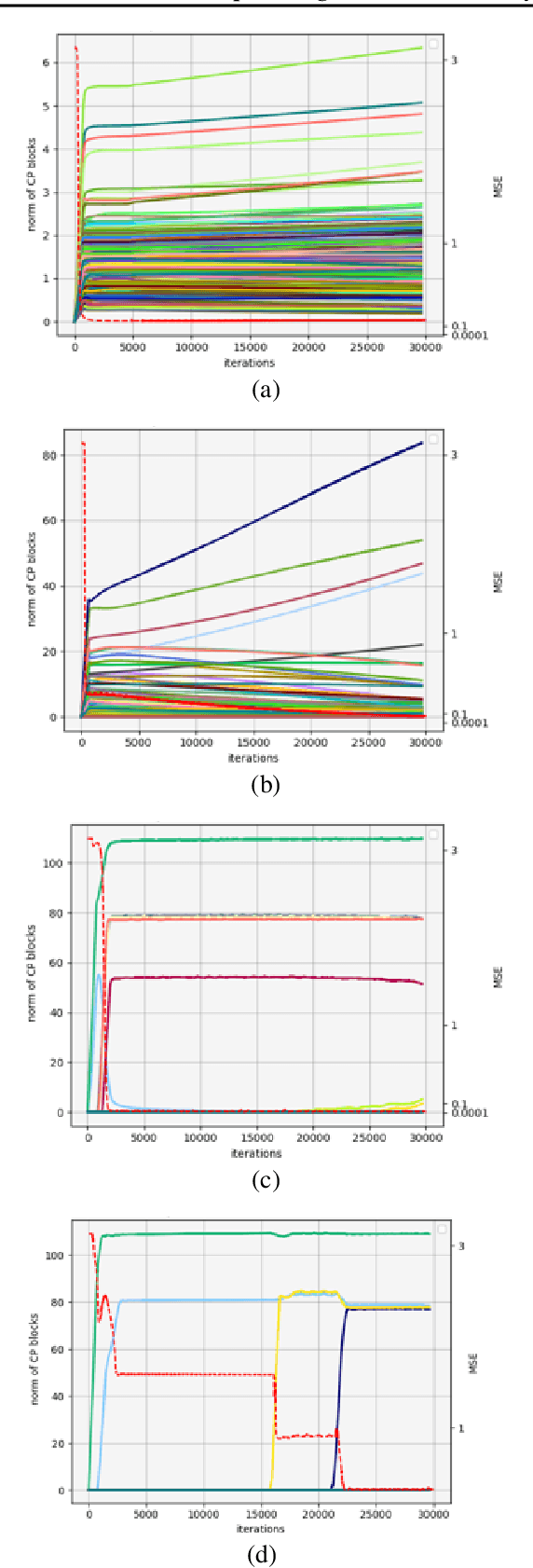
We study the implicit regularization effects of deep learning in tensor factorization. While implicit regularization in deep matrix and 'shallow' tensor factorization via linear and certain type of non-linear neural networks promotes low-rank solutions with at most quadratic growth, we show that its effect in deep tensor factorization grows polynomially with the depth of the network. This provides a remarkably faithful description of the observed experimental behaviour. Using numerical experiments, we demonstrate the benefits of this implicit regularization in yielding a more accurate estimation and better convergence properties.
* Proceedings of the 39th International Conference on Machine
Learning, Baltimore, Maryland, USA, PMLR 162, 2022 * Accepted to ICML 2022
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge