Large-Scale Quantum Separability Through a Reproducible Machine Learning Lens

The quantum separability problem consists in deciding whether a bipartite density matrix is entangled or separable. In this work, we propose a machine learning pipeline for finding approximate solutions for this NP-hard problem in large-scale scenarios. We provide an efficient Frank-Wolfe-based algorithm to approximately seek the nearest separable density matrix and derive a systematic way for labeling density matrices as separable or entangled, allowing us to treat quantum separability as a classification problem. Our method is applicable to any two-qudit mixed states. Numerical experiments with quantum states of 3- and 7-dimensional qudits validate the efficiency of the proposed procedure, and demonstrate that it scales up to thousands of density matrices with a high quantum entanglement detection accuracy. This takes a step towards benchmarking quantum separability to support the development of more powerful entanglement detection techniques.

Geodesic Quantum Walks

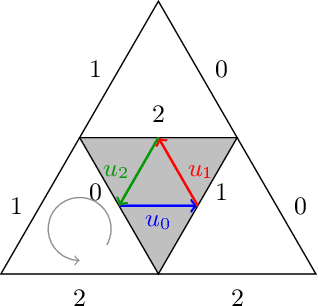
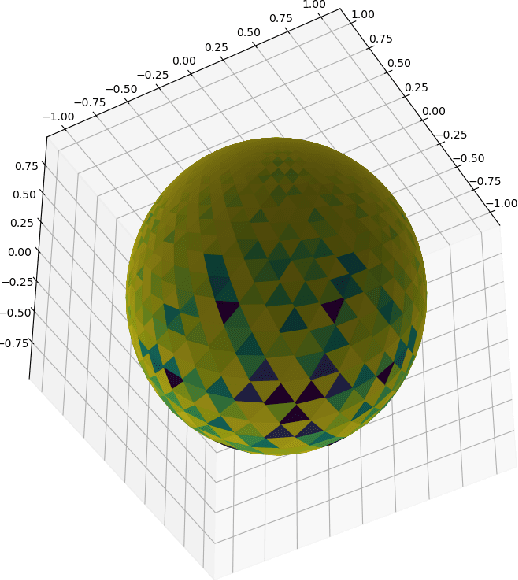
We propose a new family of discrete-spacetime quantum walks capable to propagate on any arbitrary triangulations. Moreover we also extend and generalize the duality principle introduced by one of the authors, linking continuous local deformations of a given triangulation and the inhomogeneity of the local unitaries that guide the quantum walker. We proved that in the formal continuous limit, in both space and time, this new family of quantum walks converges to the (1+2)D massless Dirac equation on curved manifolds. We believe that this result has relevance in both modelling/simulating quantum transport on discrete curved structures, such as fullerene molecules or dynamical causal triangulation, and in addressing fast and efficient optimization problems in the context of the curved space optimization methods.

Quantum Perceptron Revisited: Computational-Statistical Tradeoffs

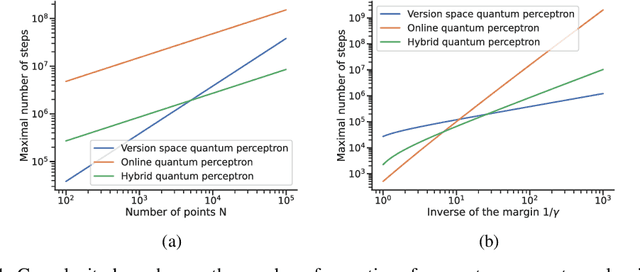
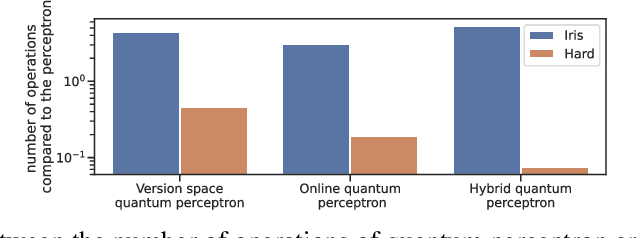
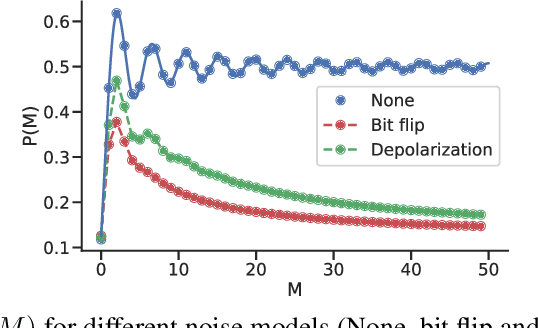
Quantum machine learning algorithms could provide significant speed-ups over their classical counterparts; however, whether they could also achieve good generalization remains unclear. Recently, two quantum perceptron models which give a quadratic improvement over the classical perceptron algorithm using Grover's search have been proposed by Wiebe et al. arXiv:1602.04799 . While the first model reduces the complexity with respect to the size of the training set, the second one improves the bound on the number of mistakes made by the perceptron. In this paper, we introduce a hybrid quantum-classical perceptron algorithm with lower complexity and better generalization ability than the classical perceptron. We show a quadratic improvement over the classical perceptron in both the number of samples and the margin of the data. We derive a bound on the expected error of the hypothesis returned by our algorithm, which compares favorably to the one obtained with the classical online perceptron. We use numerical experiments to illustrate the trade-off between computational complexity and statistical accuracy in quantum perceptron learning and discuss some of the key practical issues surrounding the implementation of quantum perceptron models into near-term quantum devices, whose practical implementation represents a serious challenge due to inherent noise. However, the potential benefits make correcting this worthwhile.

Quantum Bandits

We consider the quantum version of the bandit problem known as {\em best arm identification} (BAI). We first propose a quantum modeling of the BAI problem, which assumes that both the learning agent and the environment are quantum; we then propose an algorithm based on quantum amplitude amplification to solve BAI. We formally analyze the behavior of the algorithm on all instances of the problem and we show, in particular, that it is able to get the optimal solution quadratically faster than what is known to hold in the classical case.

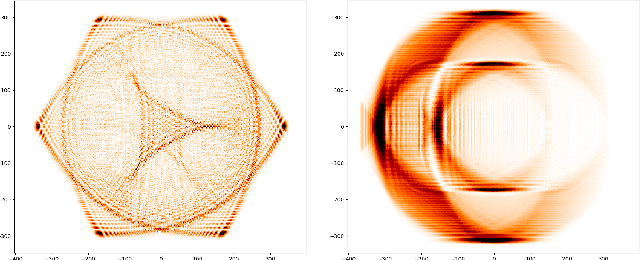
Quantum Walk over a triangular lattice subject to Pachner move

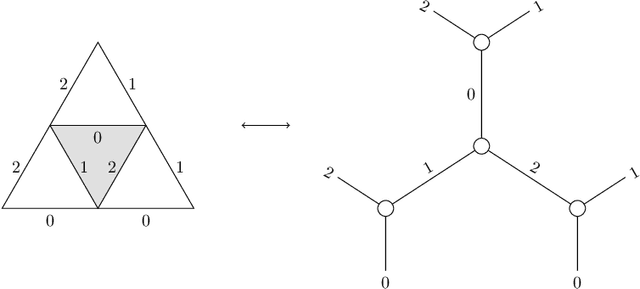
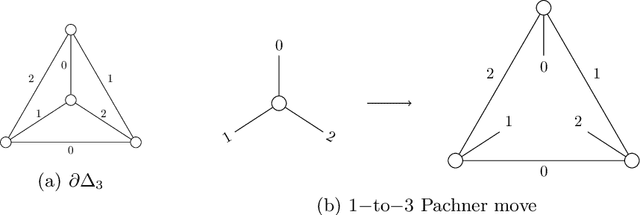
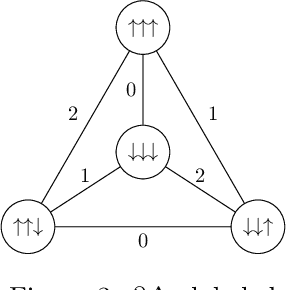
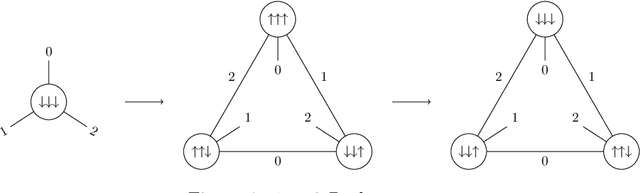
We present a $2\mathrm{-dimensional}$ quantum walker on curved discrete surfaces with dynamical geometry. This walker extends the quantum walker over the fixed triangular lattice introduced in [PRA, 97(6):062111, 2018]. We write the discrete equations of the walker on an arbitrary triangulation, whose flat spacetime limit recovers the Dirac equation in (2+1)-dimension. The geometry is changed through Pachner moves, allowing the surface to transform into any topologically equivalent surface, starting from a flat space. We present the first theoretical model which couple in a non-linear fashion the dynamics of the walker and the dynamical lattice. Numerical simulations show that both the number of wells and the local curvature grows as $t^a e^{-b t^2}$ and that in long time flatness emerge, in agreement with theory. We also prove that the global behaviour is invariant under random fluctuations of the discrete metrics.