Quentin Aristote
Quantum Walk over a triangular lattice subject to Pachner move
Aug 12, 2019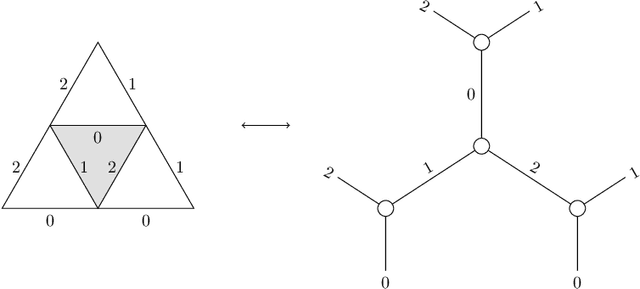
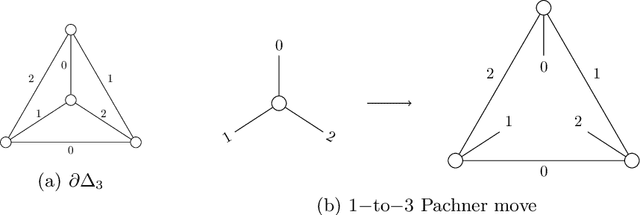
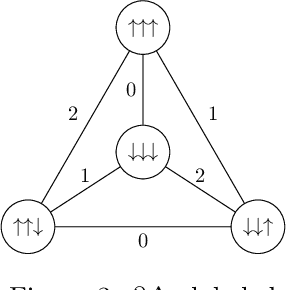
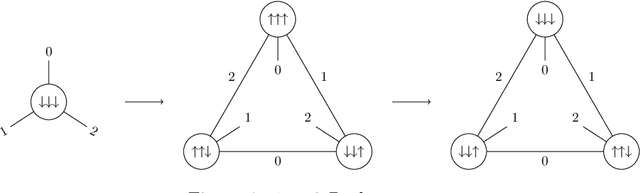
Abstract:We present a $2\mathrm{-dimensional}$ quantum walker on curved discrete surfaces with dynamical geometry. This walker extends the quantum walker over the fixed triangular lattice introduced in [PRA, 97(6):062111, 2018]. We write the discrete equations of the walker on an arbitrary triangulation, whose flat spacetime limit recovers the Dirac equation in (2+1)-dimension. The geometry is changed through Pachner moves, allowing the surface to transform into any topologically equivalent surface, starting from a flat space. We present the first theoretical model which couple in a non-linear fashion the dynamics of the walker and the dynamical lattice. Numerical simulations show that both the number of wells and the local curvature grows as $t^a e^{-b t^2}$ and that in long time flatness emerge, in agreement with theory. We also prove that the global behaviour is invariant under random fluctuations of the discrete metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge