Investigating the Sensitivity of Pre-trained Audio Embeddings to Common Effects

In recent years, foundation models have significantly advanced data-driven systems across various domains. Yet, their underlying properties, especially when functioning as feature extractors, remain under-explored. In this paper, we investigate the sensitivity to audio effects of audio embeddings extracted from widely-used foundation models, including OpenL3, PANNs, and CLAP. We focus on audio effects as the source of sensitivity due to their prevalent presence in large audio datasets. By applying parameterized audio effects (gain, low-pass filtering, reverberation, and bitcrushing), we analyze the correlation between the deformation trajectories and the effect strength in the embedding space. We propose to quantify the dimensionality and linearizability of the deformation trajectories induced by audio effects using canonical correlation analysis. We find that there exists a direction along which the embeddings move monotonically as the audio effect strength increases, but that the subspace containing the displacements is generally high-dimensional. This shows that pre-trained audio embeddings do not globally linearize the effects. Our empirical results on instrument classification downstream tasks confirm that projecting out the estimated deformation directions cannot generally improve the robustness of pre-trained embeddings to audio effects.

Geodesic Quantum Walks

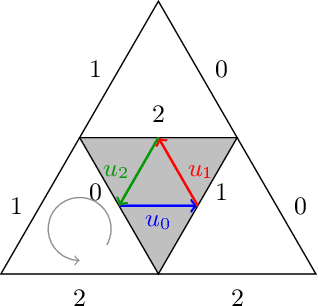
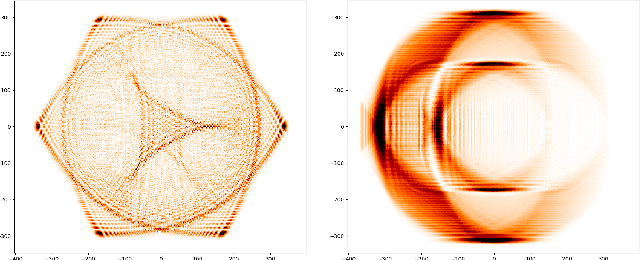
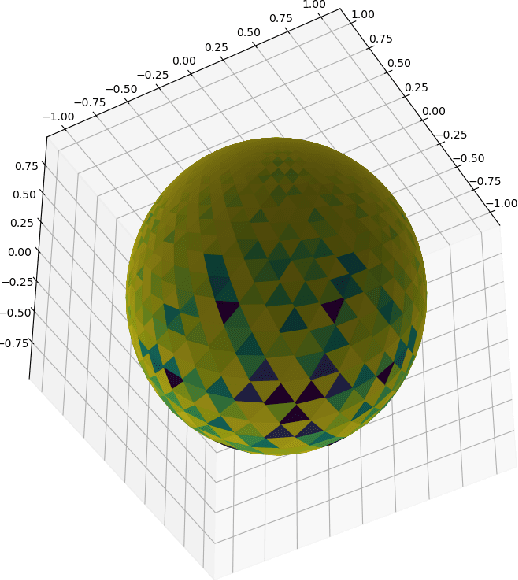
We propose a new family of discrete-spacetime quantum walks capable to propagate on any arbitrary triangulations. Moreover we also extend and generalize the duality principle introduced by one of the authors, linking continuous local deformations of a given triangulation and the inhomogeneity of the local unitaries that guide the quantum walker. We proved that in the formal continuous limit, in both space and time, this new family of quantum walks converges to the (1+2)D massless Dirac equation on curved manifolds. We believe that this result has relevance in both modelling/simulating quantum transport on discrete curved structures, such as fullerene molecules or dynamical causal triangulation, and in addressing fast and efficient optimization problems in the context of the curved space optimization methods.