Operator-valued Kernels for Learning from Functional Response Data

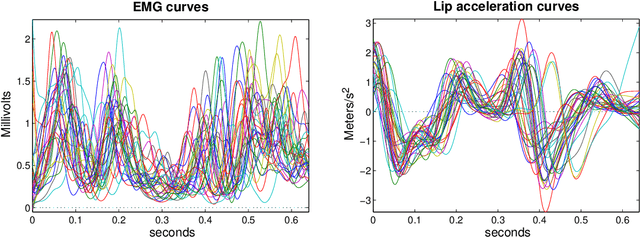
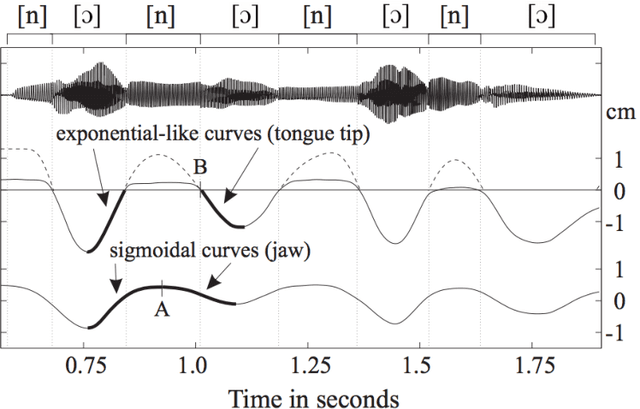
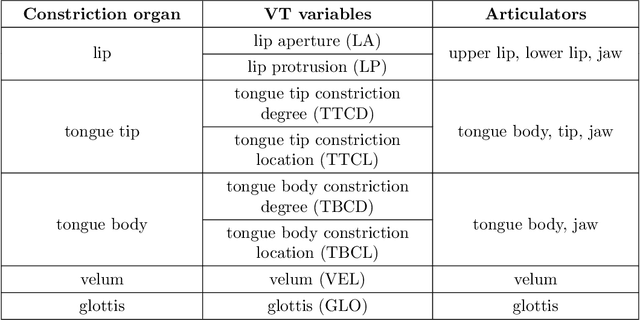
In this paper we consider the problems of supervised classification and regression in the case where attributes and labels are functions: a data is represented by a set of functions, and the label is also a function. We focus on the use of reproducing kernel Hilbert space theory to learn from such functional data. Basic concepts and properties of kernel-based learning are extended to include the estimation of function-valued functions. In this setting, the representer theorem is restated, a set of rigorously defined infinite-dimensional operator-valued kernels that can be valuably applied when the data are functions is described, and a learning algorithm for nonlinear functional data analysis is introduced. The methodology is illustrated through speech and audio signal processing experiments.

Multiple functional regression with both discrete and continuous covariates

In this paper we present a nonparametric method for extending functional regression methodology to the situation where more than one functional covariate is used to predict a functional response. Borrowing the idea from Kadri et al. (2010a), the method, which support mixed discrete and continuous explanatory variables, is based on estimating a function-valued function in reproducing kernel Hilbert spaces by virtue of positive operator-valued kernels.

Functional Regularized Least Squares Classi cation with Operator-valued Kernels

Although operator-valued kernels have recently received increasing interest in various machine learning and functional data analysis problems such as multi-task learning or functional regression, little attention has been paid to the understanding of their associated feature spaces. In this paper, we explore the potential of adopting an operator-valued kernel feature space perspective for the analysis of functional data. We then extend the Regularized Least Squares Classification (RLSC) algorithm to cover situations where there are multiple functions per observation. Experiments on a sound recognition problem show that the proposed method outperforms the classical RLSC algorithm.

Optimal Policies Search for Sensor Management

This paper introduces a new approach to solve sensor management problems. Classically sensor management problems can be well formalized as Partially-Observed Markov Decision Processes (POMPD). The original approach developped here consists in deriving the optimal parameterized policy based on a stochastic gradient estimation. We assume in this work that it is possible to learn the optimal policy off-line (in simulation) using models of the environement and of the sensor(s). The learned policy can then be used to manage the sensor(s). In order to approximate the gradient in a stochastic context, we introduce a new method to approximate the gradient, based on Infinitesimal Perturbation Approximation (IPA). The effectiveness of this general framework is illustrated by the managing of an Electronically Scanned Array Radar. First simulations results are finally proposed.