Personalized Convolutional Dictionary Learning of Physiological Time Series

Human physiological signals tend to exhibit both global and local structures: the former are shared across a population, while the latter reflect inter-individual variability. For instance, kinetic measurements of the gait cycle during locomotion present common characteristics, although idiosyncrasies may be observed due to biomechanical disposition or pathology. To better represent datasets with local-global structure, this work extends Convolutional Dictionary Learning (CDL), a popular method for learning interpretable representations, or dictionaries, of time-series data. In particular, we propose Personalized CDL (PerCDL), in which a local dictionary models local information as a personalized spatiotemporal transformation of a global dictionary. The transformation is learnable and can combine operations such as time warping and rotation. Formal computational and statistical guarantees for PerCDL are provided and its effectiveness on synthetic and real human locomotion data is demonstrated.

Riemannian Metric Learning: Closer to You than You Imagine

Riemannian metric learning is an emerging field in machine learning, unlocking new ways to encode complex data structures beyond traditional distance metric learning. While classical approaches rely on global distances in Euclidean space, they often fall short in capturing intrinsic data geometry. Enter Riemannian metric learning: a powerful generalization that leverages differential geometry to model the data according to their underlying Riemannian manifold. This approach has demonstrated remarkable success across diverse domains, from causal inference and optimal transport to generative modeling and representation learning. In this review, we bridge the gap between classical metric learning and Riemannian geometry, providing a structured and accessible overview of key methods, applications, and recent advances. We argue that Riemannian metric learning is not merely a technical refinement but a fundamental shift in how we think about data representations. Thus, this review should serve as a valuable resource for researchers and practitioners interested in exploring Riemannian metric learning and convince them that it is closer to them than they might imagine-both in theory and in practice.

Stochastic Approximation with Biased MCMC for Expectation Maximization

The expectation maximization (EM) algorithm is a widespread method for empirical Bayesian inference, but its expectation step (E-step) is often intractable. Employing a stochastic approximation scheme with Markov chain Monte Carlo (MCMC) can circumvent this issue, resulting in an algorithm known as MCMC-SAEM. While theoretical guarantees for MCMC-SAEM have previously been established, these results are restricted to the case where asymptotically unbiased MCMC algorithms are used. In practice, MCMC-SAEM is often run with asymptotically biased MCMC, for which the consequences are theoretically less understood. In this work, we fill this gap by analyzing the asymptotics and non-asymptotics of SAEM with biased MCMC steps, particularly the effect of bias. We also provide numerical experiments comparing the Metropolis-adjusted Langevin algorithm (MALA), which is asymptotically unbiased, and the unadjusted Langevin algorithm (ULA), which is asymptotically biased, on synthetic and real datasets. Experimental results show that ULA is more stable with respect to the choice of Langevin stepsize and can sometimes result in faster convergence.

On the convergence of dynamic implementations of Hamiltonian Monte Carlo and No U-Turn Samplers

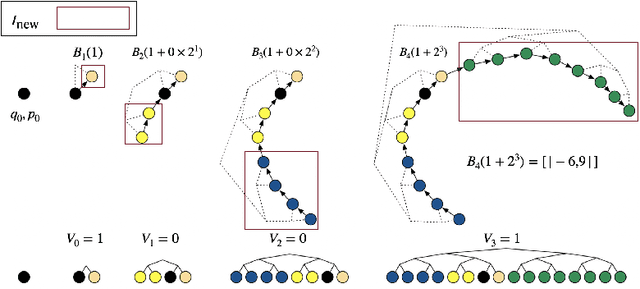
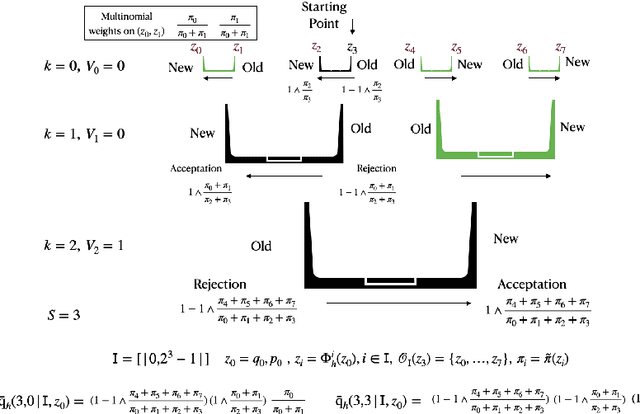
There is substantial empirical evidence about the success of dynamic implementations of Hamiltonian Monte Carlo (HMC), such as the No U-Turn Sampler (NUTS), in many challenging inference problems but theoretical results about their behavior are scarce. The aim of this paper is to fill this gap. More precisely, we consider a general class of MCMC algorithms we call dynamic HMC. We show that this general framework encompasses NUTS as a particular case, implying the invariance of the target distribution as a by-product. Second, we establish conditions under which NUTS is irreducible and aperiodic and as a corrolary ergodic. Under conditions similar to the ones existing for HMC, we also show that NUTS is geometrically ergodic. Finally, we improve existing convergence results for HMC showing that this method is ergodic without any boundedness condition on the stepsize and the number of leapfrog steps, in the case where the target is a perturbation of a Gaussian distribution.