Zuheng Xu
Tuning Sequential Monte Carlo Samplers via Greedy Incremental Divergence Minimization
Mar 19, 2025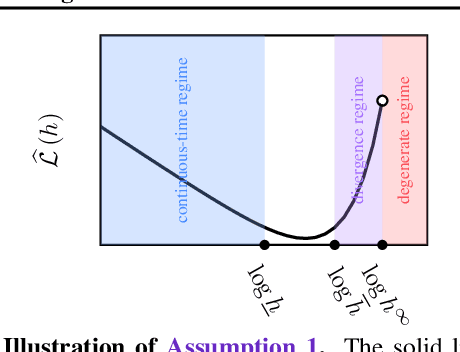

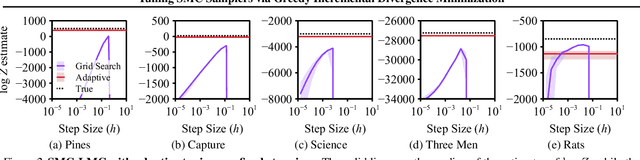
Abstract:The performance of sequential Monte Carlo (SMC) samplers heavily depends on the tuning of the Markov kernels used in the path proposal. For SMC samplers with unadjusted Markov kernels, standard tuning objectives, such as the Metropolis-Hastings acceptance rate or the expected-squared jump distance, are no longer applicable. While stochastic gradient-based end-to-end optimization has been explored for tuning SMC samplers, they often incur excessive training costs, even for tuning just the kernel step sizes. In this work, we propose a general adaptation framework for tuning the Markov kernels in SMC samplers by minimizing the incremental Kullback-Leibler (KL) divergence between the proposal and target paths. For step size tuning, we provide a gradient- and tuning-free algorithm that is generally applicable for kernels such as Langevin Monte Carlo (LMC). We further demonstrate the utility of our approach by providing a tailored scheme for tuning \textit{kinetic} LMC used in SMC samplers. Our implementations are able to obtain a full \textit{schedule} of tuned parameters at the cost of a few vanilla SMC runs, which is a fraction of gradient-based approaches.
Turning Waste into Wealth: Leveraging Low-Quality Samples for Enhancing Continuous Conditional Generative Adversarial Networks
Aug 20, 2023Abstract:Continuous Conditional Generative Adversarial Networks (CcGANs) enable generative modeling conditional on continuous scalar variables (termed regression labels). However, they can produce subpar fake images due to limited training data. Although Negative Data Augmentation (NDA) effectively enhances unconditional and class-conditional GANs by introducing anomalies into real training images, guiding the GANs away from low-quality outputs, its impact on CcGANs is limited, as it fails to replicate negative samples that may occur during the CcGAN sampling. We present a novel NDA approach called Dual-NDA specifically tailored for CcGANs to address this problem. Dual-NDA employs two types of negative samples: visually unrealistic images generated from a pre-trained CcGAN and label-inconsistent images created by manipulating real images' labels. Leveraging these negative samples, we introduce a novel discriminator objective alongside a modified CcGAN training algorithm. Empirical analysis on UTKFace and Steering Angle reveals that Dual-NDA consistently enhances the visual fidelity and label consistency of fake images generated by CcGANs, exhibiting a substantial performance gain over the vanilla NDA. Moreover, by applying Dual-NDA, CcGANs demonstrate a remarkable advancement beyond the capabilities of state-of-the-art conditional GANs and diffusion models, establishing a new pinnacle of performance.
Embracing the chaos: analysis and diagnosis of numerical instability in variational flows
Jul 12, 2023Abstract:In this paper, we investigate the impact of numerical instability on the reliability of sampling, density evaluation, and evidence lower bound (ELBO) estimation in variational flows. We first empirically demonstrate that common flows can exhibit a catastrophic accumulation of error: the numerical flow map deviates significantly from the exact map -- which affects sampling -- and the numerical inverse flow map does not accurately recover the initial input -- which affects density and ELBO computations. Surprisingly though, we find that results produced by flows are often accurate enough for applications despite the presence of serious numerical instability. In this work, we treat variational flows as dynamical systems, and leverage shadowing theory to elucidate this behavior via theoretical guarantees on the error of sampling, density evaluation, and ELBO estimation. Finally, we develop and empirically test a diagnostic procedure that can be used to validate results produced by numerically unstable flows in practice.
Ergodic variational flows
May 16, 2022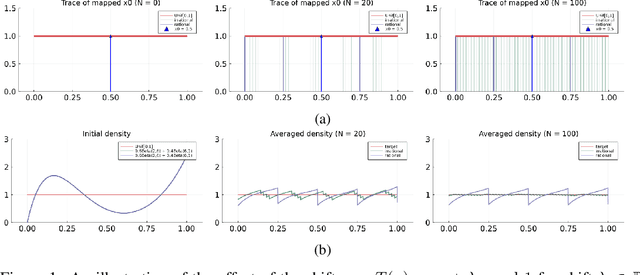
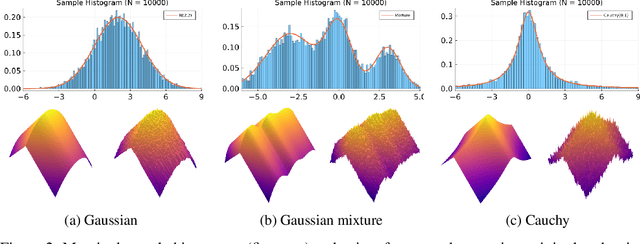
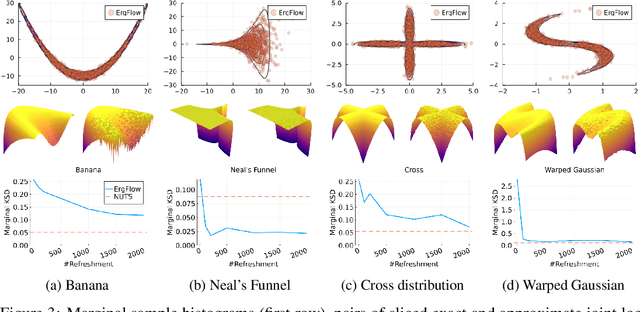
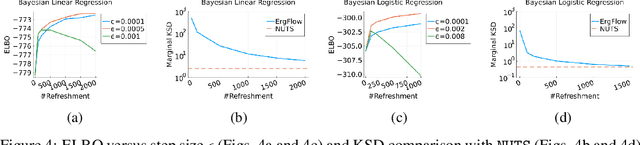
Abstract:This work presents a new class of variational family -- ergodic variational flows -- that not only enables tractable i.i.d. sampling and density evaluation, but also comes with MCMC-like convergence guarantees. Ergodic variational flows consist of a mixture of repeated applications of a measure-preserving and ergodic map to an initial reference distribution. We provide mild conditions under which the variational distribution converges weakly and in total variation to the target as the number of steps in the flow increases; this convergence holds regardless of the value of variational parameters, although different parameter values may result in faster or slower convergence. Further, we develop a particular instantiation of the general family using Hamiltonian dynamics combined with deterministic momentum refreshment. Simulated and real data experiments provide an empirical verification of the convergence theory and demonstrate that samples produced by the method are of comparable quality to a state-of-the-art MCMC method.
Bayesian inference via sparse Hamiltonian flows
Mar 11, 2022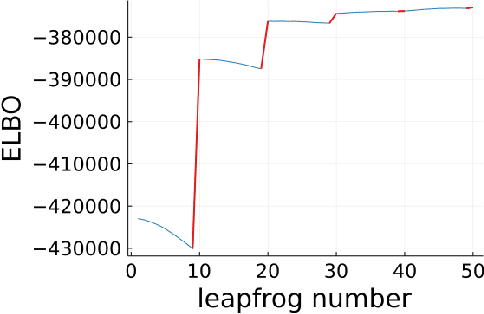

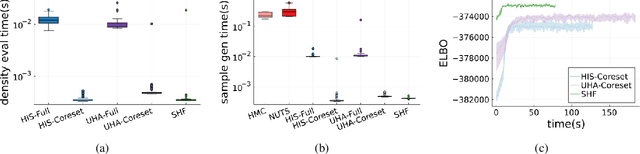
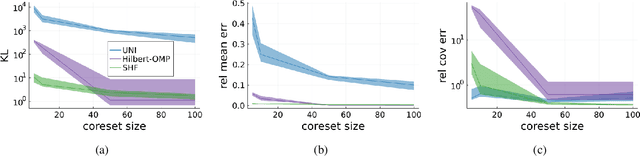
Abstract:A Bayesian coreset is a small, weighted subset of data that replaces the full dataset during Bayesian inference, with the goal of reducing computational cost. Although past work has shown empirically that there often exists a coreset with low inferential error, efficiently constructing such a coreset remains a challenge. Current methods tend to be slow, require a secondary inference step after coreset construction, and do not provide bounds on the data marginal evidence. In this work, we introduce a new method -- sparse Hamiltonian flows -- that addresses all three of these challenges. The method involves first subsampling the data uniformly, and then optimizing a Hamiltonian flow parametrized by coreset weights and including periodic momentum quasi-refreshment steps. Theoretical results show that the method enables an exponential compression of the dataset in a representative model, and that the quasi-refreshment steps reduce the KL divergence to the target. Real and synthetic experiments demonstrate that sparse Hamiltonian flows provide accurate posterior approximations with significantly reduced runtime compared with competing dynamical-system-based inference methods.
Distilling and Transferring Knowledge via cGAN-generated Samples for Image Classification and Regression
May 01, 2021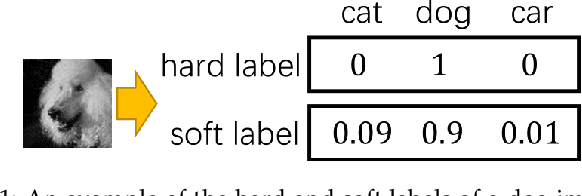
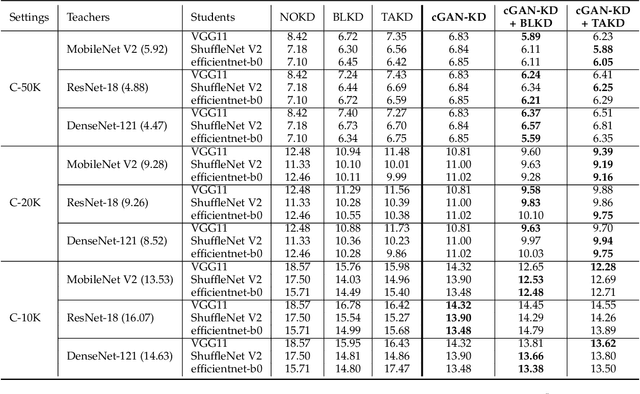
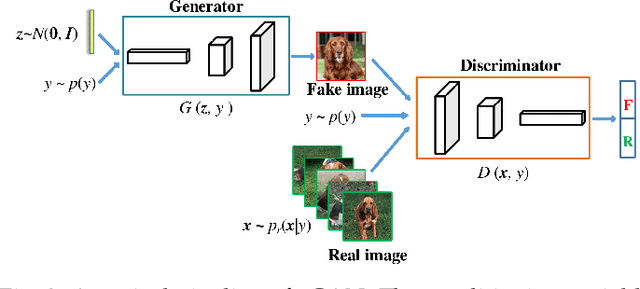
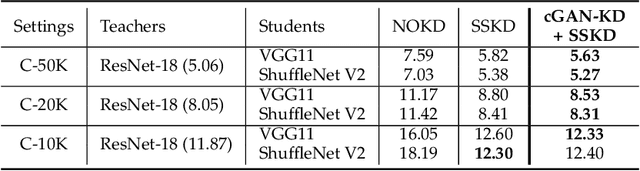
Abstract:Knowledge distillation (KD) has been actively studied for image classification tasks in deep learning, aiming to improve the performance of a student model based on the knowledge from a teacher model. However, there have been very few efforts for applying KD in image regression with a scalar response, and there is no KD method applicable to both tasks. Moreover, existing KD methods often require a practitioner to carefully choose or adjust the teacher and student architectures, making these methods less scalable in practice. Furthermore, although KD is usually conducted in scenarios with limited labeled data, very few techniques are developed to alleviate such data insufficiency. To solve the above problems in an all-in-one manner, we propose in this paper a unified KD framework based on conditional generative adversarial networks (cGANs), termed cGAN-KD. Fundamentally different from existing KD methods, cGAN-KD distills and transfers knowledge from a teacher model to a student model via cGAN-generated samples. This unique mechanism makes cGAN-KD suitable for both classification and regression tasks, compatible with other KD methods, and insensitive to the teacher and student architectures. Also, benefiting from the recent advances in cGAN methodology and our specially designed subsampling and filtering procedures, cGAN-KD also performs well when labeled data are scarce. An error bound of a student model trained in the cGAN-KD framework is derived in this work, which theoretically explains why cGAN-KD takes effect and guides the implementation of cGAN-KD in practice. Extensive experiments on CIFAR-10 and Tiny-ImageNet show that we can incorporate state-of-the-art KD methods into the cGAN-KD framework to reach a new state of the art. Also, experiments on RC-49 and UTKFace demonstrate the effectiveness of cGAN-KD in image regression tasks, where existing KD methods are inapplicable.
The computational asymptotics of Gaussian variational inference
Apr 13, 2021
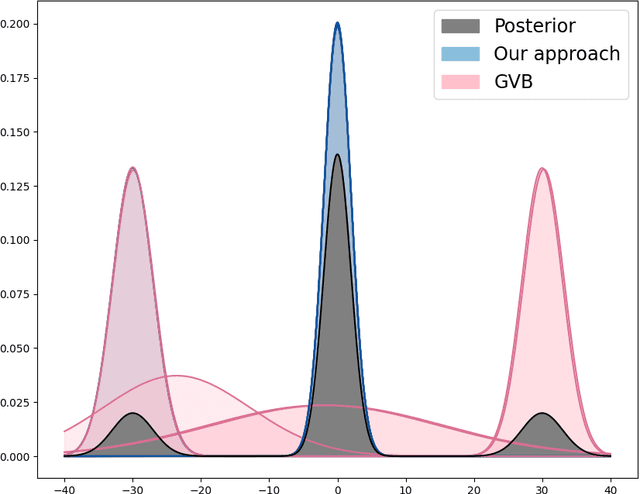
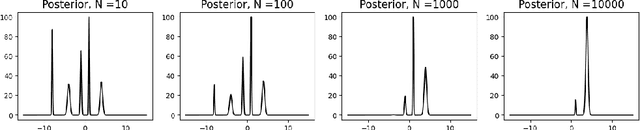
Abstract:Variational inference is a popular alternative to Markov chain Monte Carlo methods that constructs a Bayesian posterior approximation by minimizing a discrepancy to the true posterior within a pre-specified family. This converts Bayesian inference into an optimization problem, enabling the use of simple and scalable stochastic optimization algorithms. However, a key limitation of variational inference is that the optimal approximation is typically not tractable to compute; even in simple settings the problem is nonconvex. Thus, recently developed statistical guarantees -- which all involve the (data) asymptotic properties of the optimal variational distribution -- are not reliably obtained in practice. In this work, we provide two major contributions: a theoretical analysis of the asymptotic convexity properties of variational inference in the popular setting with a Gaussian family; and consistent stochastic variational inference (CSVI), an algorithm that exploits these properties to find the optimal approximation in the asymptotic regime. CSVI consists of a tractable initialization procedure that finds the local basin of the optimal solution, and a scaled gradient descent algorithm that stays locally confined to that basin. Experiments on nonconvex synthetic and real-data examples show that compared with standard stochastic gradient descent, CSVI improves the likelihood of obtaining the globally optimal posterior approximation.
CcGAN: Continuous Conditional Generative Adversarial Networks for Image Generation
Nov 15, 2020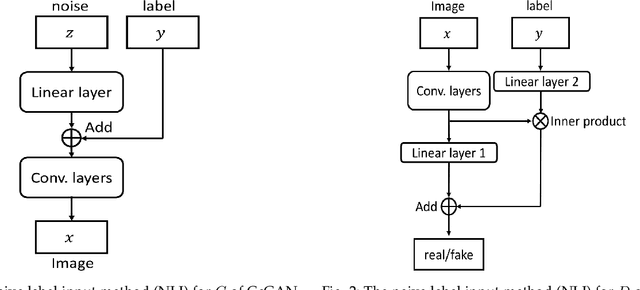

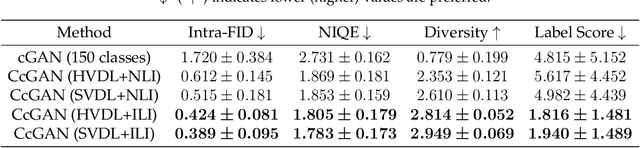

Abstract:This work proposes the continuous conditional generative adversarial network (CcGAN), the first generative model for image generation conditional on continuous, scalar conditions (termed regression labels). Existing conditional GANs (cGANs) are mainly designed for categorical conditions (e.g., class labels); conditioning on regression labels is mathematically distinct and raises two fundamental problems: (P1) Since there may be very few (even zero) real images for some regression labels, minimizing existing empirical versions of cGAN losses (a.k.a. empirical cGAN losses) often fails in practice; (P2) Since regression labels are scalar and infinitely many, conventional label input methods are not applicable. The proposed CcGAN solves the above problems, respectively, by (S1) reformulating existing empirical cGAN losses to be appropriate for the continuous scenario; and (S2) proposing a naive label input (NLI) method and an improved label input (ILI) method to incorporate regression labels into the generator and the discriminator. The reformulation in (S1) leads to two novel empirical discriminator losses, termed the hard vicinal discriminator loss (HVDL) and the soft vicinal discriminator loss (SVDL) respectively, and a novel empirical generator loss. The error bounds of a discriminator trained with HVDL and SVDL are derived under mild assumptions in this work. Two new benchmark datasets (RC-49 and Cell-200) and a novel evaluation metric (Sliding Fr\'echet Inception Distance) are also proposed for this continuous scenario. Our experiments on the Circular 2-D Gaussians, RC-49, UTKFace, Cell-200, and Steering Angle datasets show that CcGAN can generate diverse, high-quality samples from the image distribution conditional on a given regression label. Moreover, in these experiments, CcGAN substantially outperforms cGAN both visually and quantitatively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge