Ergodic variational flows
Paper and Code
May 16, 2022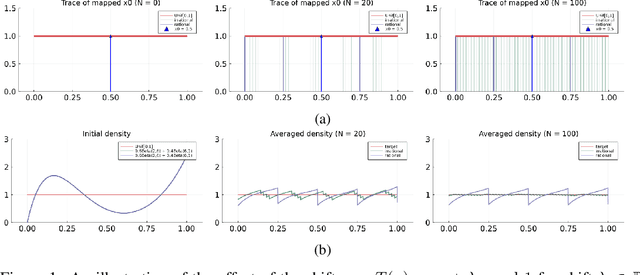
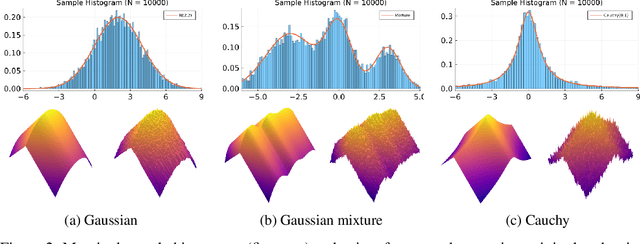
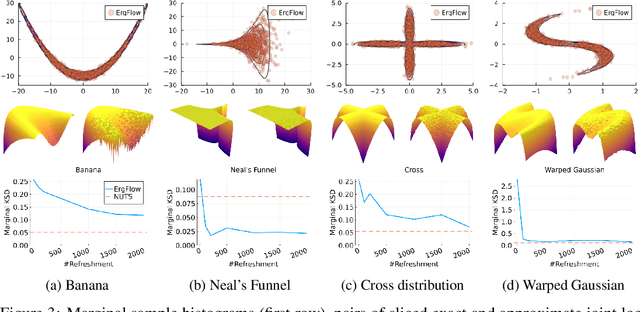
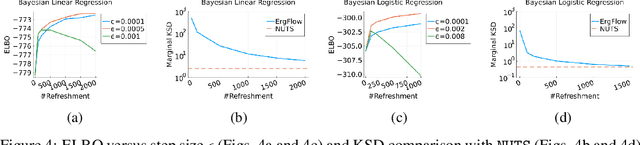
This work presents a new class of variational family -- ergodic variational flows -- that not only enables tractable i.i.d. sampling and density evaluation, but also comes with MCMC-like convergence guarantees. Ergodic variational flows consist of a mixture of repeated applications of a measure-preserving and ergodic map to an initial reference distribution. We provide mild conditions under which the variational distribution converges weakly and in total variation to the target as the number of steps in the flow increases; this convergence holds regardless of the value of variational parameters, although different parameter values may result in faster or slower convergence. Further, we develop a particular instantiation of the general family using Hamiltonian dynamics combined with deterministic momentum refreshment. Simulated and real data experiments provide an empirical verification of the convergence theory and demonstrate that samples produced by the method are of comparable quality to a state-of-the-art MCMC method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge