Data-Adaptive Dimensional Analysis for Accurate Interpolation and Extrapolation in Computer Experiments

Dimensional analysis (DA) pays attention to fundamental physical dimensions such as length and mass when modelling scientific and engineering systems. It goes back at least a century to Buckingham's Pi theorem, which characterizes a scientifically meaningful model in terms of a limited number of dimensionless variables. The methodology has only been exploited relatively recently by statisticians for design and analysis of experiments, however, and computer experiments in particular. The basic idea is to build models in terms of new dimensionless quantities derived from the original input and output variables. A scientifically valid formulation has the potential for improved prediction accuracy in principle, but the implementation of DA is far from straightforward. There can be a combinatorial number of possible models satisfying the conditions of the theory. Empirical approaches for finding effective derived variables will be described, and improvements in prediction accuracy will be demonstrated. As DA's dimensionless quantities for a statistical model typically compare the original variables rather than use their absolute magnitudes, DA is less dependent on the choice of experimental ranges in the training data. Hence, we are also able to illustrate sustained accuracy gains even when extrapolating substantially outside the training data.

Distilling and Transferring Knowledge via cGAN-generated Samples for Image Classification and Regression

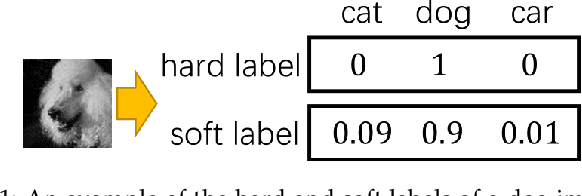
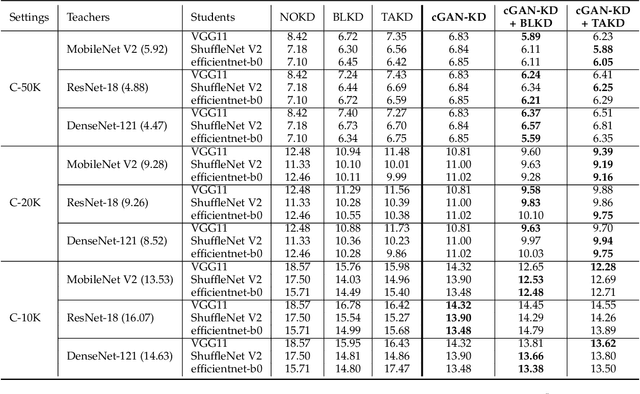
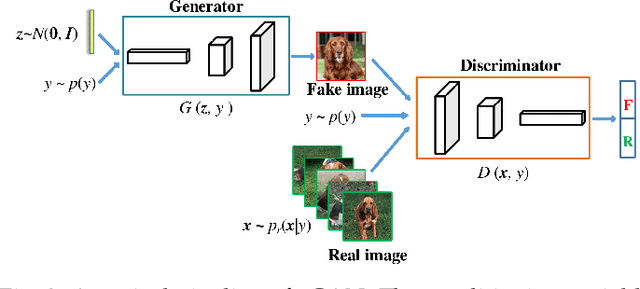
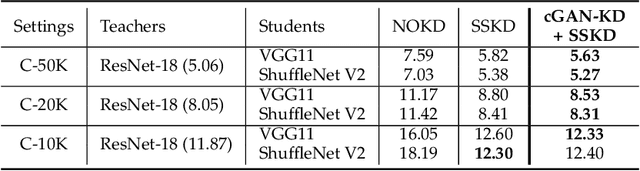
Knowledge distillation (KD) has been actively studied for image classification tasks in deep learning, aiming to improve the performance of a student model based on the knowledge from a teacher model. However, there have been very few efforts for applying KD in image regression with a scalar response, and there is no KD method applicable to both tasks. Moreover, existing KD methods often require a practitioner to carefully choose or adjust the teacher and student architectures, making these methods less scalable in practice. Furthermore, although KD is usually conducted in scenarios with limited labeled data, very few techniques are developed to alleviate such data insufficiency. To solve the above problems in an all-in-one manner, we propose in this paper a unified KD framework based on conditional generative adversarial networks (cGANs), termed cGAN-KD. Fundamentally different from existing KD methods, cGAN-KD distills and transfers knowledge from a teacher model to a student model via cGAN-generated samples. This unique mechanism makes cGAN-KD suitable for both classification and regression tasks, compatible with other KD methods, and insensitive to the teacher and student architectures. Also, benefiting from the recent advances in cGAN methodology and our specially designed subsampling and filtering procedures, cGAN-KD also performs well when labeled data are scarce. An error bound of a student model trained in the cGAN-KD framework is derived in this work, which theoretically explains why cGAN-KD takes effect and guides the implementation of cGAN-KD in practice. Extensive experiments on CIFAR-10 and Tiny-ImageNet show that we can incorporate state-of-the-art KD methods into the cGAN-KD framework to reach a new state of the art. Also, experiments on RC-49 and UTKFace demonstrate the effectiveness of cGAN-KD in image regression tasks, where existing KD methods are inapplicable.

Efficient Subsampling for Generating High-Quality Images from Conditional Generative Adversarial Networks

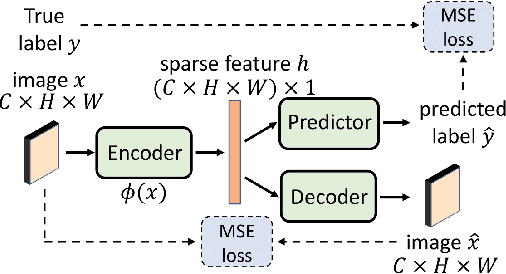
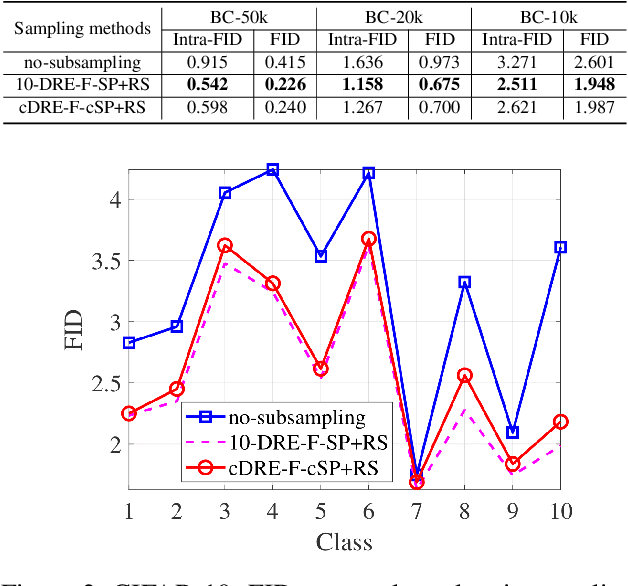
Subsampling unconditional generative adversarial networks (GANs) to improve the overall image quality has been studied recently. However, these methods often require high training costs (e.g., storage space, parameter tuning) and may be inefficient or even inapplicable for subsampling conditional GANs, such as class-conditional GANs and continuous conditional GANs (CcGANs), when the condition has many distinct values. In this paper, we propose an efficient method called conditional density ratio estimation in feature space with conditional Softplus loss (cDRE-F-cSP). With cDRE-F-cSP, we estimate an image's conditional density ratio based on a novel conditional Softplus (cSP) loss in the feature space learned by a specially designed ResNet-34 or sparse autoencoder. We then derive the error bound of a conditional density ratio model trained with the proposed cSP loss. Finally, we propose a rejection sampling scheme, termed cDRE-F-cSP+RS, which can subsample both class-conditional GANs and CcGANs efficiently. An extra filtering scheme is also developed for CcGANs to increase the label consistency. Experiments on CIFAR-10 and Tiny-ImageNet datasets show that cDRE-F-cSP+RS can substantially improve the Intra-FID and FID scores of BigGAN. Experiments on RC-49 and UTKFace datasets demonstrate that cDRE-F-cSP+RS also improves Intra-FID, Diversity, and Label Score of CcGANs. Moreover, to show the high efficiency of cDRE-F-cSP+RS, we compare it with the state-of-the-art unconditional subsampling method (i.e., DRE-F-SP+RS). With comparable or even better performance, cDRE-F-cSP+RS only requires about \textbf{10}\% and \textbf{1.7}\% of the training costs spent respectively on CIFAR-10 and UTKFace by DRE-F-SP+RS.

CcGAN: Continuous Conditional Generative Adversarial Networks for Image Generation

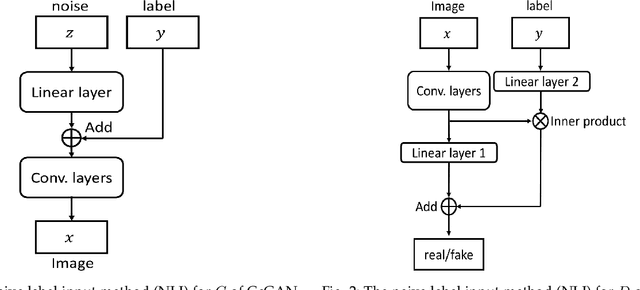
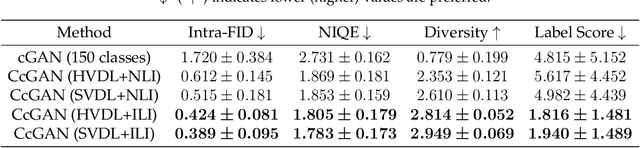
This work proposes the continuous conditional generative adversarial network (CcGAN), the first generative model for image generation conditional on continuous, scalar conditions (termed regression labels). Existing conditional GANs (cGANs) are mainly designed for categorical conditions (e.g., class labels); conditioning on regression labels is mathematically distinct and raises two fundamental problems: (P1) Since there may be very few (even zero) real images for some regression labels, minimizing existing empirical versions of cGAN losses (a.k.a. empirical cGAN losses) often fails in practice; (P2) Since regression labels are scalar and infinitely many, conventional label input methods are not applicable. The proposed CcGAN solves the above problems, respectively, by (S1) reformulating existing empirical cGAN losses to be appropriate for the continuous scenario; and (S2) proposing a naive label input (NLI) method and an improved label input (ILI) method to incorporate regression labels into the generator and the discriminator. The reformulation in (S1) leads to two novel empirical discriminator losses, termed the hard vicinal discriminator loss (HVDL) and the soft vicinal discriminator loss (SVDL) respectively, and a novel empirical generator loss. The error bounds of a discriminator trained with HVDL and SVDL are derived under mild assumptions in this work. Two new benchmark datasets (RC-49 and Cell-200) and a novel evaluation metric (Sliding Fr\'echet Inception Distance) are also proposed for this continuous scenario. Our experiments on the Circular 2-D Gaussians, RC-49, UTKFace, Cell-200, and Steering Angle datasets show that CcGAN can generate diverse, high-quality samples from the image distribution conditional on a given regression label. Moreover, in these experiments, CcGAN substantially outperforms cGAN both visually and quantitatively.

Classification Beats Regression: Counting of Cells from Greyscale Microscopic Images based on Annotation-free Training Samples

Modern methods often formulate the counting of cells from microscopic images as a regression problem and more or less rely on expensive, manually annotated training images (e.g., dot annotations indicating the centroids of cells or segmentation masks identifying the contours of cells). This work proposes a supervised learning framework based on classification-oriented convolutional neural networks (CNNs) to count cells from greyscale microscopic images without using annotated training images. In this framework, we formulate the cell counting task as an image classification problem, where the cell counts are taken as class labels. This formulation has its limitation when some cell counts in the test stage do not appear in the training data. Moreover, the ordinal relation among cell counts is not utilized. To deal with these limitations, we propose a simple but effective data augmentation (DA) method to synthesize images for the unseen cell counts. We also introduce an ensemble method, which can not only moderate the influence of unseen cell counts but also utilize the ordinal information to improve the prediction accuracy. This framework outperforms many modern cell counting methods and won the data analysis competition (Case Study 1: Counting Cells From Microscopic Images https://ssc.ca/en/case-study/case-study-1-counting-cells-microscopic-images) of the 47th Annual Meeting of the Statistical Society of Canada (SSC). Our code is available at https://github.com/anno2020/CellCount_TinyBBBC005.

Subsampling Generative Adversarial Networks: Density Ratio Estimation in Feature Space with Softplus Loss

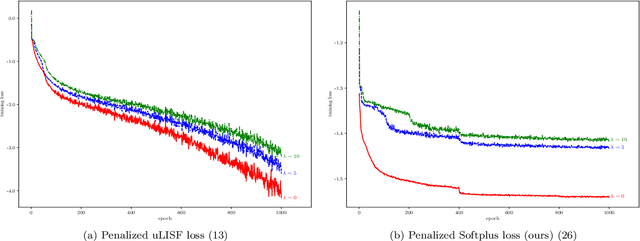
Filtering out unrealistic images from trained generative adversarial networks (GANs) has attracted considerable attention recently. Two density ratio based subsampling methods---Discriminator Rejection Sampling (DRS) and Metropolis-Hastings GAN (MH-GAN)---were recently proposed, and their effectiveness in improving GANs was demonstrated on multiple datasets. However, DRS and MH-GAN are based on discriminator based density ratio estimation (DRE) methods, so they may not work well if the discriminator in the trained GAN is far from optimal. Moreover, they do not apply to some GANs (e.g., MMD-GAN). In this paper, we propose a novel Softplus (SP) loss for DRE. Based on it, we develop a sample-based DRE method in a feature space learned by a specially designed and pre-trained ResNet-34 (DRE-F-SP). We derive the rate of convergence of a density ratio model trained under the SP loss. Then, we propose three different density ratio subsampling methods (DRE-F-SP+RS, DRE-F-SP+MH, and DRE-F-SP+SIR) for GANs based on DRE-F-SP. Our subsampling methods do not rely on the optimality of the discriminator and are suitable for all types of GANs. We empirically show our subsampling approach can substantially outperform DRS and MH-GAN on a synthetic dataset and the CIFAR-10 dataset, using multiple GANs.

Sequential Computer Experimental Design for Estimating an Extreme Probability or Quantile

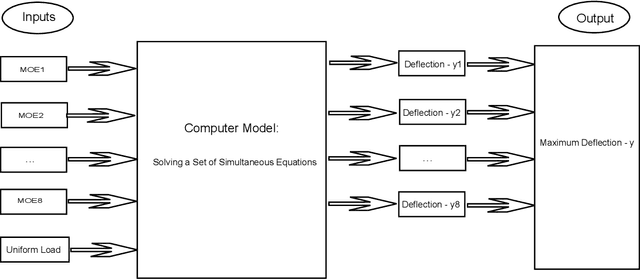
A computer code can simulate a system's propagation of variation from random inputs to output measures of quality. Our aim here is to estimate a critical output tail probability or quantile without a large Monte Carlo experiment. Instead, we build a statistical surrogate for the input-output relationship with a modest number of evaluations and then sequentially add further runs, guided by a criterion to improve the estimate. We compare two criteria in the literature. Moreover, we investigate two practical questions: how to design the initial code runs and how to model the input distribution. Hence, we close the gap between the theory of sequential design and its application.

Bayesian Optimization Using Monotonicity Information and Its Application in Machine Learning Hyperparameter

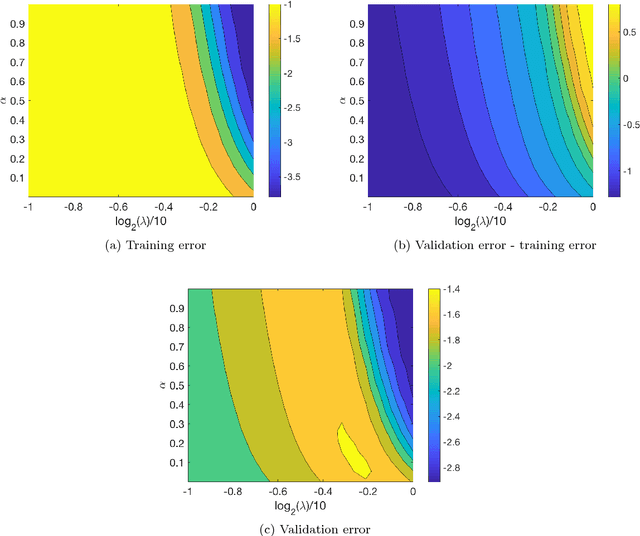
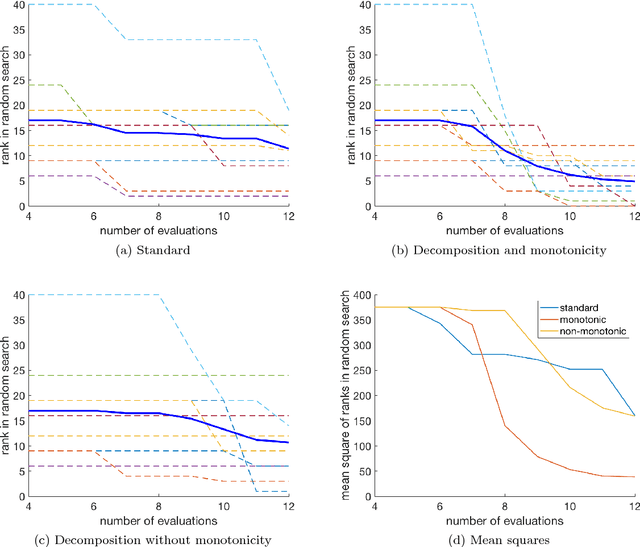
We propose an algorithm for a family of optimization problems where the objective can be decomposed as a sum of functions with monotonicity properties. The motivating problem is optimization of hyperparameters of machine learning algorithms, where we argue that the objective, validation error, can be decomposed as monotonic functions of the hyperparameters. Our proposed algorithm adapts Bayesian optimization methods to incorporate the monotonicity constraints. We illustrate the advantages of exploiting monotonicity using illustrative examples and demonstrate the improvements in optimization efficiency for some machine learning hyperparameter tuning applications.

Regression Phalanxes

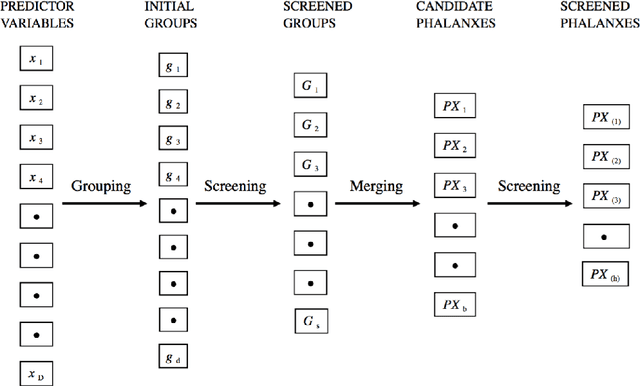
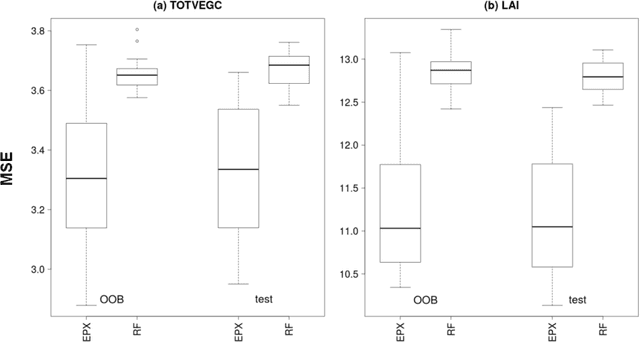
Tomal et al. (2015) introduced the notion of "phalanxes" in the context of rare-class detection in two-class classification problems. A phalanx is a subset of features that work well for classification tasks. In this paper, we propose a different class of phalanxes for application in regression settings. We define a "Regression Phalanx" - a subset of features that work well together for prediction. We propose a novel algorithm which automatically chooses Regression Phalanxes from high-dimensional data sets using hierarchical clustering and builds a prediction model for each phalanx for further ensembling. Through extensive simulation studies and several real-life applications in various areas (including drug discovery, chemical analysis of spectra data, microarray analysis and climate projections) we show that an ensemble of Regression Phalanxes improves prediction accuracy when combined with effective prediction methods like Lasso or Random Forests.

Ensembling classification models based on phalanxes of variables with applications in drug discovery

Statistical detection of a rare class of objects in a two-class classification problem can pose several challenges. Because the class of interest is rare in the training data, there is relatively little information in the known class response labels for model building. At the same time the available explanatory variables are often moderately high dimensional. In the four assays of our drug-discovery application, compounds are active or not against a specific biological target, such as lung cancer tumor cells, and active compounds are rare. Several sets of chemical descriptor variables from computational chemistry are available to classify the active versus inactive class; each can have up to thousands of variables characterizing molecular structure of the compounds. The statistical challenge is to make use of the richness of the explanatory variables in the presence of scant response information. Our algorithm divides the explanatory variables into subsets adaptively and passes each subset to a base classifier. The various base classifiers are then ensembled to produce one model to rank new objects by their estimated probabilities of belonging to the rare class of interest. The essence of the algorithm is to choose the subsets such that variables in the same group work well together; we call such groups phalanxes.