Regularized K-means through hard-thresholding

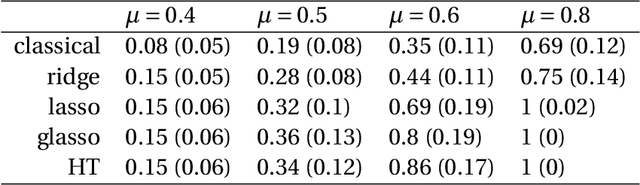
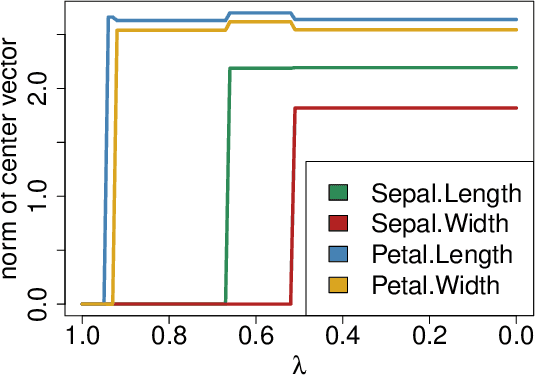
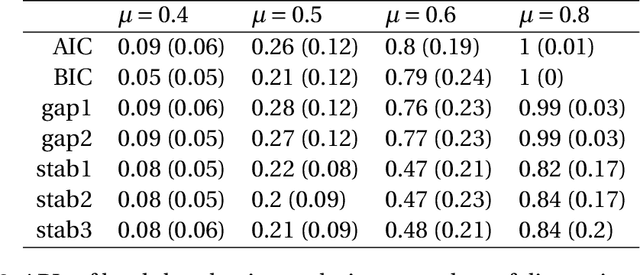
We study a framework of regularized $K$-means methods based on direct penalization of the size of the cluster centers. Different penalization strategies are considered and compared through simulation and theoretical analysis. Based on the results, we propose HT $K$-means, which uses an $\ell_0$ penalty to induce sparsity in the variables. Different techniques for selecting the tuning parameter are discussed and compared. The proposed method stacks up favorably with the most popular regularized $K$-means methods in an extensive simulation study. Finally, HT $K$-means is applied to several real data examples. Graphical displays are presented and used in these examples to gain more insight into the datasets.

Multi-rank Sparse Hierarchical Clustering

There has been a surge in the number of large and flat data sets - data sets containing a large number of features and a relatively small number of observations - due to the growing ability to collect and store information in medical research and other fields. Hierarchical clustering is a widely used clustering tool. In hierarchical clustering, large and flat data sets may allow for a better coverage of clustering features (features that help explain the true underlying clusters) but, such data sets usually include a large fraction of noise features (non-clustering features) that may hide the underlying clusters. Witten and Tibshirani (2010) proposed a sparse hierarchical clustering framework to cluster the observations using an adaptively chosen subset of the features, however, we show that this framework has some limitations when the data sets contain clustering features with complex structure. In this paper, we propose the Multi-rank sparse hierarchical clustering (MrSHC). We show that, using simulation studies and real data examples, MrSHC produces superior feature selection and clustering performance comparing to the classical (of-the-shelf) hierarchical clustering and the existing sparse hierarchical clustering framework.

Regression Phalanxes

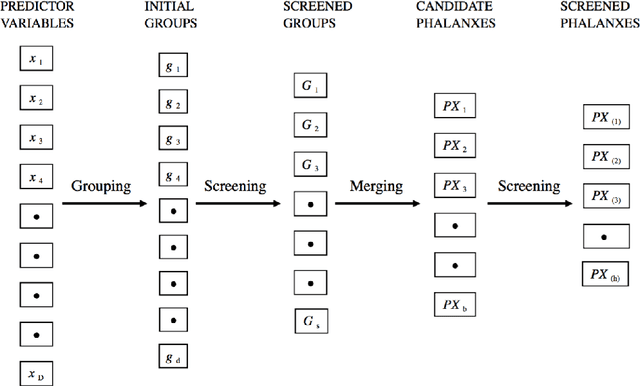
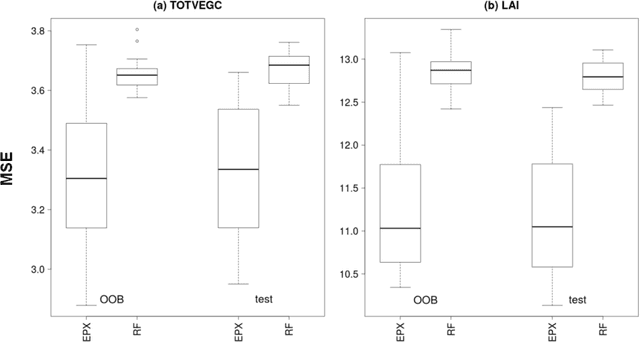
Tomal et al. (2015) introduced the notion of "phalanxes" in the context of rare-class detection in two-class classification problems. A phalanx is a subset of features that work well for classification tasks. In this paper, we propose a different class of phalanxes for application in regression settings. We define a "Regression Phalanx" - a subset of features that work well together for prediction. We propose a novel algorithm which automatically chooses Regression Phalanxes from high-dimensional data sets using hierarchical clustering and builds a prediction model for each phalanx for further ensembling. Through extensive simulation studies and several real-life applications in various areas (including drug discovery, chemical analysis of spectra data, microarray analysis and climate projections) we show that an ensemble of Regression Phalanxes improves prediction accuracy when combined with effective prediction methods like Lasso or Random Forests.

Ensembling classification models based on phalanxes of variables with applications in drug discovery

Statistical detection of a rare class of objects in a two-class classification problem can pose several challenges. Because the class of interest is rare in the training data, there is relatively little information in the known class response labels for model building. At the same time the available explanatory variables are often moderately high dimensional. In the four assays of our drug-discovery application, compounds are active or not against a specific biological target, such as lung cancer tumor cells, and active compounds are rare. Several sets of chemical descriptor variables from computational chemistry are available to classify the active versus inactive class; each can have up to thousands of variables characterizing molecular structure of the compounds. The statistical challenge is to make use of the richness of the explanatory variables in the presence of scant response information. Our algorithm divides the explanatory variables into subsets adaptively and passes each subset to a base classifier. The various base classifiers are then ensembled to produce one model to rank new objects by their estimated probabilities of belonging to the rare class of interest. The essence of the algorithm is to choose the subsets such that variables in the same group work well together; we call such groups phalanxes.