Bayesian Optimization Using Monotonicity Information and Its Application in Machine Learning Hyperparameter
Paper and Code
Feb 16, 2018

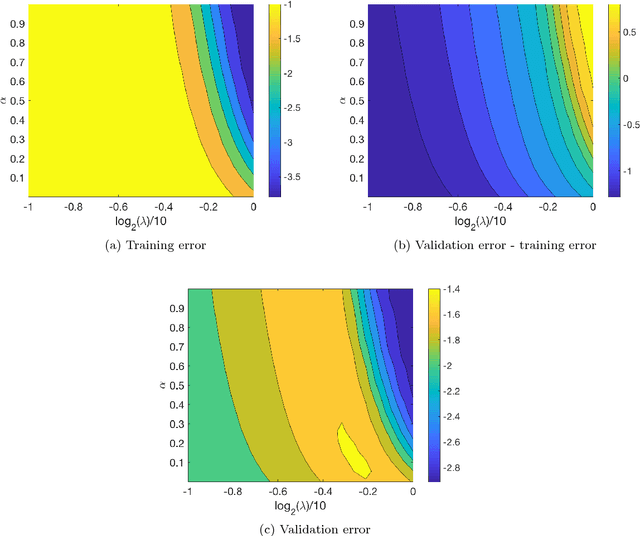
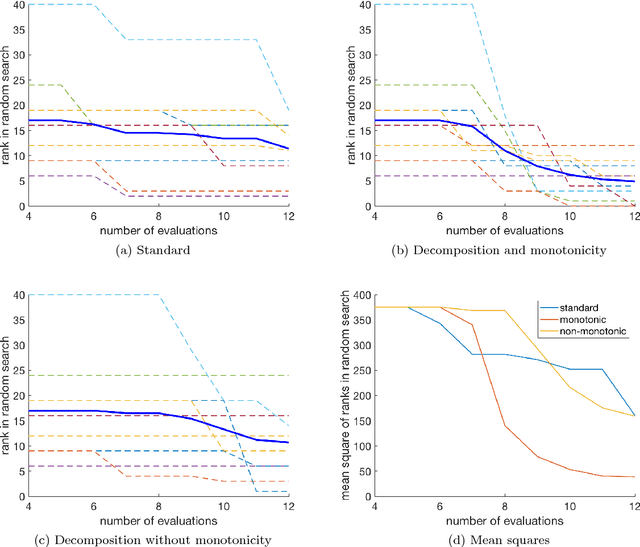
We propose an algorithm for a family of optimization problems where the objective can be decomposed as a sum of functions with monotonicity properties. The motivating problem is optimization of hyperparameters of machine learning algorithms, where we argue that the objective, validation error, can be decomposed as monotonic functions of the hyperparameters. Our proposed algorithm adapts Bayesian optimization methods to incorporate the monotonicity constraints. We illustrate the advantages of exploiting monotonicity using illustrative examples and demonstrate the improvements in optimization efficiency for some machine learning hyperparameter tuning applications.
* Citation style errors fixed
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge