Bayesian inference via sparse Hamiltonian flows
Paper and Code
Mar 11, 2022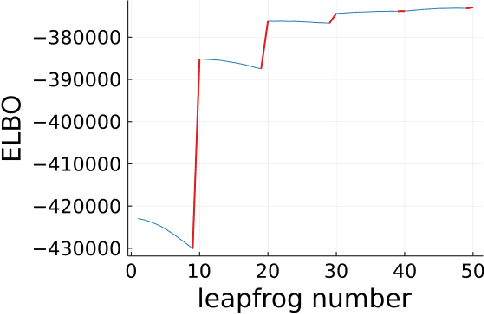

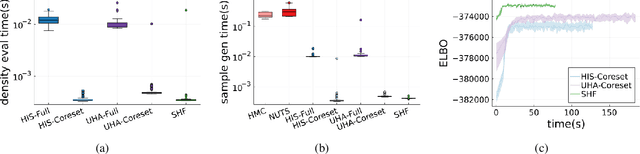
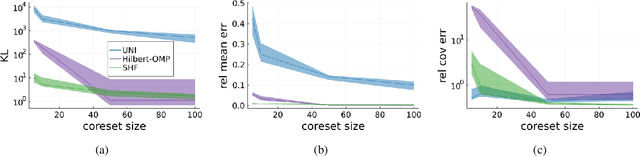
A Bayesian coreset is a small, weighted subset of data that replaces the full dataset during Bayesian inference, with the goal of reducing computational cost. Although past work has shown empirically that there often exists a coreset with low inferential error, efficiently constructing such a coreset remains a challenge. Current methods tend to be slow, require a secondary inference step after coreset construction, and do not provide bounds on the data marginal evidence. In this work, we introduce a new method -- sparse Hamiltonian flows -- that addresses all three of these challenges. The method involves first subsampling the data uniformly, and then optimizing a Hamiltonian flow parametrized by coreset weights and including periodic momentum quasi-refreshment steps. Theoretical results show that the method enables an exponential compression of the dataset in a representative model, and that the quasi-refreshment steps reduce the KL divergence to the target. Real and synthetic experiments demonstrate that sparse Hamiltonian flows provide accurate posterior approximations with significantly reduced runtime compared with competing dynamical-system-based inference methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge