AutoStep: Locally adaptive involutive MCMC

Many common Markov chain Monte Carlo (MCMC) kernels can be formulated using a deterministic involutive proposal with a step size parameter. Selecting an appropriate step size is often a challenging task in practice; and for complex multiscale targets, there may not be one choice of step size that works well globally. In this work, we address this problem with a novel class of involutive MCMC methods -- AutoStep MCMC -- that selects an appropriate step size at each iteration adapted to the local geometry of the target distribution. We prove that AutoStep MCMC is $\pi$-invariant and has other desirable properties under mild assumptions on the target distribution $\pi$ and involutive proposal. Empirical results examine the effect of various step size selection design choices, and show that AutoStep MCMC is competitive with state-of-the-art methods in terms of effective sample size per unit cost on a range of challenging target distributions.

MCMC-driven learning

This paper is intended to appear as a chapter for the Handbook of Markov Chain Monte Carlo. The goal of this chapter is to unify various problems at the intersection of Markov chain Monte Carlo (MCMC) and machine learning$\unicode{x2014}$which includes black-box variational inference, adaptive MCMC, normalizing flow construction and transport-assisted MCMC, surrogate-likelihood MCMC, coreset construction for MCMC with big data, Markov chain gradient descent, Markovian score climbing, and more$\unicode{x2014}$within one common framework. By doing so, the theory and methods developed for each may be translated and generalized.

Slice Sampling for General Completely Random Measures

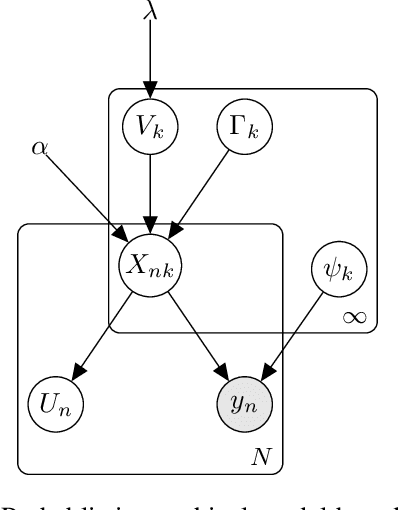
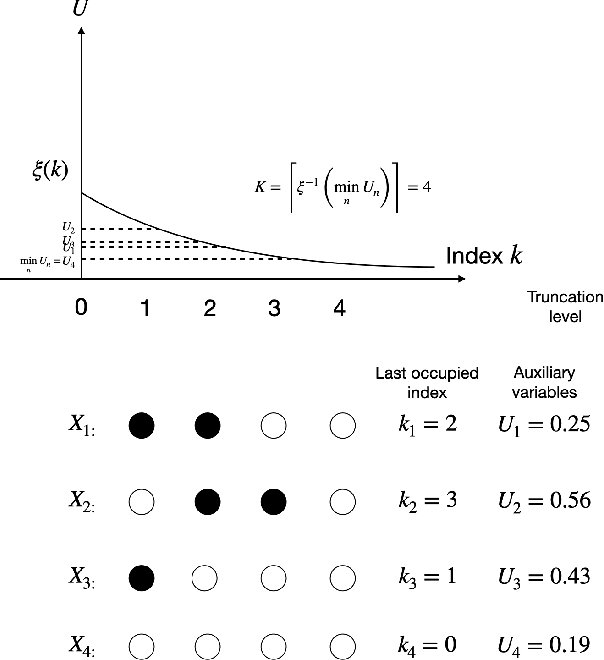
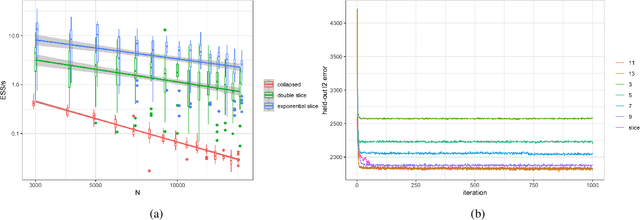
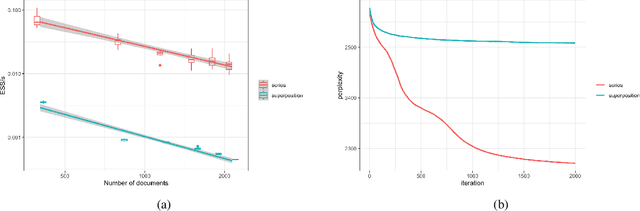
Completely random measures provide a principled approach to creating flexible unsupervised models, where the number of latent features is infinite and the number of features that influence the data grows with the size of the data set. Due to the infinity the latent features, posterior inference requires either marginalization---resulting in dependence structures that prevent efficient computation via parallelization and conjugacy---or finite truncation, which arbitrarily limits the flexibility of the model. In this paper we present a novel Markov chain Monte Carlo algorithm for posterior inference that adaptively sets the truncation level using auxiliary slice variables, enabling efficient, parallelized computation without sacrificing flexibility. In contrast to past work that achieved this on a model-by-model basis, we provide a general recipe that is applicable to the broad class of completely random measure-based priors. The efficacy of the proposed algorithm is evaluated on several popular nonparametric models, demonstrating a higher effective sample size per second compared to algorithms using marginalization as well as a higher predictive performance compared to models employing fixed truncations.

Particle-Gibbs Sampling For Bayesian Feature Allocation Models

Bayesian feature allocation models are a popular tool for modelling data with a combinatorial latent structure. Exact inference in these models is generally intractable and so practitioners typically apply Markov Chain Monte Carlo (MCMC) methods for posterior inference. The most widely used MCMC strategies rely on an element wise Gibbs update of the feature allocation matrix. These element wise updates can be inefficient as features are typically strongly correlated. To overcome this problem we have developed a Gibbs sampler that can update an entire row of the feature allocation matrix in a single move. However, this sampler is impractical for models with a large number of features as the computational complexity scales exponentially in the number of features. We develop a Particle Gibbs sampler that targets the same distribution as the row wise Gibbs updates, but has computational complexity that only grows linearly in the number of features. We compare the performance of our proposed methods to the standard Gibbs sampler using synthetic data from a range of feature allocation models. Our results suggest that row wise updates using the PG methodology can significantly improve the performance of samplers for feature allocation models.

Blang: Bayesian declarative modelling of arbitrary data structures

Consider a Bayesian inference problem where a variable of interest does not take values in a Euclidean space. These "non-standard" data structures are in reality fairly common. They are frequently used in problems involving latent discrete factor models, networks, and domain specific problems such as sequence alignments and reconstructions, pedigrees, and phylogenies. In principle, Bayesian inference should be particularly well-suited in such scenarios, as the Bayesian paradigm provides a principled way to obtain confidence assessment for random variables of any type. However, much of the recent work on making Bayesian analysis more accessible and computationally efficient has focused on inference in Euclidean spaces. In this paper, we introduce Blang, a domain specific language (DSL) and library aimed at bridging this gap. Blang allows users to perform Bayesian analysis on arbitrary data types while using a declarative syntax similar to BUGS. Blang is augmented with intuitive language additions to invent data types of the user's choosing. To perform inference at scale on such arbitrary state spaces, Blang leverages recent advances in parallelizable, non-reversible Markov chain Monte Carlo methods.

Analysis of high-dimensional Continuous Time Markov Chains using the Local Bouncy Particle Sampler

Sampling the parameters of high-dimensional Continuous Time Markov Chains (CTMC) is a challenging problem with important applications in many fields of applied statistics. In this work a recently proposed type of non-reversible rejection-free Markov Chain Monte Carlo (MCMC) sampler, the Bouncy Particle Sampler (BPS), is brought to bear to this problem. BPS has demonstrated its favorable computational efficiency compared with state-of-the-art MCMC algorithms, however to date applications to real-data scenario were scarce. An important aspect of the practical implementation of BPS is the simulation of event times. Default implementations use conservative thinning bounds. Such bounds can slow down the algorithm and limit the computational performance. Our paper develops an algorithm with an exact analytical solution to the random event times in the context of CTMCs. Our local version of BPS algorithm takes advantage of the sparse structure in the target factor graph and we also provide a framework for assessing the computational complexity of local BPS algorithms.

Scalable Metropolis-Hastings for Exact Bayesian Inference with Large Datasets

Bayesian inference via standard Markov Chain Monte Carlo (MCMC) methods such as Metropolis-Hastings is too computationally intensive to handle large datasets, since the cost per step usually scales like $O(n)$ in the number of data points $n$. We propose the Scalable Metropolis-Hastings (SMH) kernel that exploits Gaussian concentration of the posterior to require processing on average only $O(1)$ or even $O(1/\sqrt{n})$ data points per step. This scheme is based on a combination of factorized acceptance probabilities, procedures for fast simulation of Bernoulli processes, and control variate ideas. Contrary to many MCMC subsampling schemes such as fixed step-size Stochastic Gradient Langevin Dynamics, our approach is exact insofar as the invariant distribution is the true posterior and not an approximation to it. We characterise the performance of our algorithm theoretically, and give realistic and verifiable conditions under which it is geometrically ergodic. This theory is borne out by empirical results that demonstrate overall performance benefits over standard Metropolis-Hastings and various subsampling algorithms.

Unbounded Bayesian Optimization via Regularization

Bayesian optimization has recently emerged as a popular and efficient tool for global optimization and hyperparameter tuning. Currently, the established Bayesian optimization practice requires a user-defined bounding box which is assumed to contain the optimizer. However, when little is known about the probed objective function, it can be difficult to prescribe such bounds. In this work we modify the standard Bayesian optimization framework in a principled way to allow automatic resizing of the search space. We introduce two alternative methods and compare them on two common synthetic benchmarking test functions as well as the tasks of tuning the stochastic gradient descent optimizer of a multi-layered perceptron and a convolutional neural network on MNIST.

Divide-and-Conquer with Sequential Monte Carlo

We propose a novel class of Sequential Monte Carlo (SMC) algorithms, appropriate for inference in probabilistic graphical models. This class of algorithms adopts a divide-and-conquer approach based upon an auxiliary tree-structured decomposition of the model of interest, turning the overall inferential task into a collection of recursively solved sub-problems. The proposed method is applicable to a broad class of probabilistic graphical models, including models with loops. Unlike a standard SMC sampler, the proposed Divide-and-Conquer SMC employs multiple independent populations of weighted particles, which are resampled, merged, and propagated as the method progresses. We illustrate empirically that this approach can outperform standard methods in terms of the accuracy of the posterior expectation and marginal likelihood approximations. Divide-and-Conquer SMC also opens up novel parallel implementation options and the possibility of concentrating the computational effort on the most challenging sub-problems. We demonstrate its performance on a Markov random field and on a hierarchical logistic regression problem.

An Entropy Search Portfolio for Bayesian Optimization

Bayesian optimization is a sample-efficient method for black-box global optimization. How- ever, the performance of a Bayesian optimization method very much depends on its exploration strategy, i.e. the choice of acquisition function, and it is not clear a priori which choice will result in superior performance. While portfolio methods provide an effective, principled way of combining a collection of acquisition functions, they are often based on measures of past performance which can be misleading. To address this issue, we introduce the Entropy Search Portfolio (ESP): a novel approach to portfolio construction which is motivated by information theoretic considerations. We show that ESP outperforms existing portfolio methods on several real and synthetic problems, including geostatistical datasets and simulated control tasks. We not only show that ESP is able to offer performance as good as the best, but unknown, acquisition function, but surprisingly it often gives better performance. Finally, over a wide range of conditions we find that ESP is robust to the inclusion of poor acquisition functions.