Slice Sampling for General Completely Random Measures
Paper and Code
Jun 25, 2020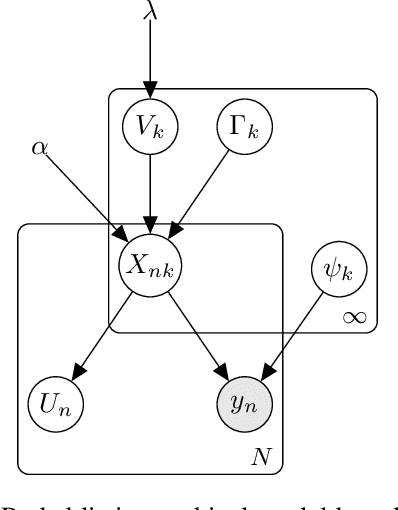
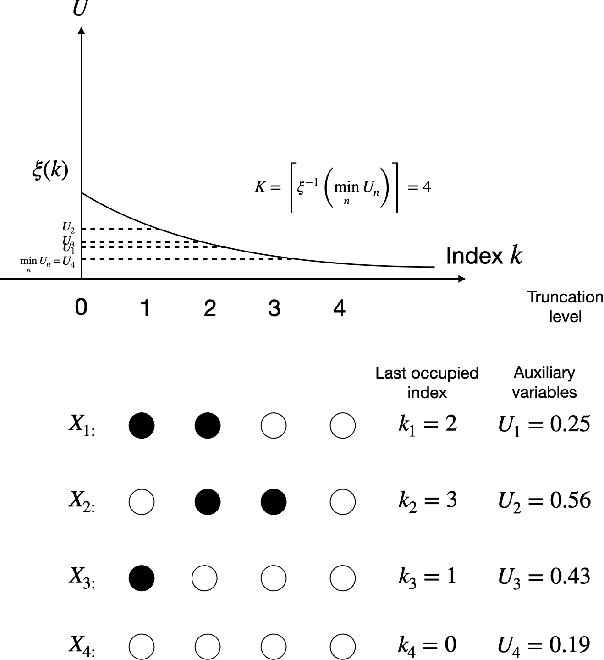
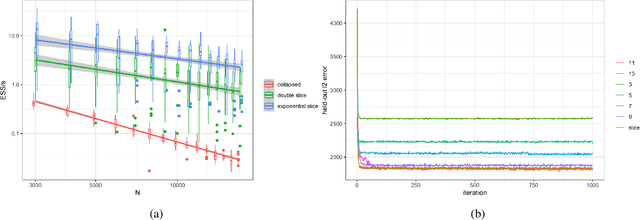
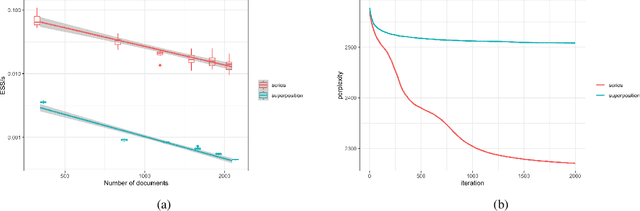
Completely random measures provide a principled approach to creating flexible unsupervised models, where the number of latent features is infinite and the number of features that influence the data grows with the size of the data set. Due to the infinity the latent features, posterior inference requires either marginalization---resulting in dependence structures that prevent efficient computation via parallelization and conjugacy---or finite truncation, which arbitrarily limits the flexibility of the model. In this paper we present a novel Markov chain Monte Carlo algorithm for posterior inference that adaptively sets the truncation level using auxiliary slice variables, enabling efficient, parallelized computation without sacrificing flexibility. In contrast to past work that achieved this on a model-by-model basis, we provide a general recipe that is applicable to the broad class of completely random measure-based priors. The efficacy of the proposed algorithm is evaluated on several popular nonparametric models, demonstrating a higher effective sample size per second compared to algorithms using marginalization as well as a higher predictive performance compared to models employing fixed truncations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge