Improving Adversarial Energy-Based Model via Diffusion Process

Generative models have shown strong generation ability while efficient likelihood estimation is less explored. Energy-based models~(EBMs) define a flexible energy function to parameterize unnormalized densities efficiently but are notorious for being difficult to train. Adversarial EBMs introduce a generator to form a minimax training game to avoid expensive MCMC sampling used in traditional EBMs, but a noticeable gap between adversarial EBMs and other strong generative models still exists. Inspired by diffusion-based models, we embedded EBMs into each denoising step to split a long-generated process into several smaller steps. Besides, we employ a symmetric Jeffrey divergence and introduce a variational posterior distribution for the generator's training to address the main challenges that exist in adversarial EBMs. Our experiments show significant improvement in generation compared to existing adversarial EBMs, while also providing a useful energy function for efficient density estimation.

Session-Based Recommendation by Exploiting Substitutable and Complementary Relationships from Multi-behavior Data

Session-based recommendation (SR) aims to dynamically recommend items to a user based on a sequence of the most recent user-item interactions. Most existing studies on SR adopt advanced deep learning methods. However, the majority only consider a special behavior type (e.g., click), while those few considering multi-typed behaviors ignore to take full advantage of the relationships between products (items). In this case, the paper proposes a novel approach, called Substitutable and Complementary Relationships from Multi-behavior Data (denoted as SCRM) to better explore the relationships between products for effective recommendation. Specifically, we firstly construct substitutable and complementary graphs based on a user's sequential behaviors in every session by jointly considering `click' and `purchase' behaviors. We then design a denoising network to remove false relationships, and further consider constraints on the two relationships via a particularly designed loss function. Extensive experiments on two e-commerce datasets demonstrate the superiority of our model over state-of-the-art methods, and the effectiveness of every component in SCRM.

Causality and Correlation Graph Modeling for Effective and Explainable Session-based Recommendation

Session-based recommendation which has been witnessed a booming interest recently, focuses on predicting a user's next interested item(s) based on an anonymous session. Most existing studies adopt complex deep learning techniques (e.g., graph neural networks) for effective session-based recommendation. However, they merely address co-occurrence between items, but fail to well distinguish causality and correlation relationship. Considering the varied interpretations and characteristics of causality and correlation relationship between items, in this study, we propose a novel method denoted as CGSR by jointly modeling causality and correlation relationship between items. In particular, we construct cause, effect and correlation graphs from sessions by simultaneously considering the false causality problem. We further design a graph neural network-based method for session-based recommendation. Extensive experiments on three datasets show that our model outperforms other state-of-the-art methods in terms of recommendation accuracy. Moreover, we further propose an explainable framework on CGSR, and demonstrate the explainability of our model via case studies on Amazon dataset.

Bounds all around: training energy-based models with bidirectional bounds

Energy-based models (EBMs) provide an elegant framework for density estimation, but they are notoriously difficult to train. Recent work has established links to generative adversarial networks, where the EBM is trained through a minimax game with a variational value function. We propose a bidirectional bound on the EBM log-likelihood, such that we maximize a lower bound and minimize an upper bound when solving the minimax game. We link one bound to a gradient penalty that stabilizes training, thereby providing grounding for best engineering practice. To evaluate the bounds we develop a new and efficient estimator of the Jacobi-determinant of the EBM generator. We demonstrate that these developments significantly stabilize training and yield high-quality density estimation and sample generation.

Generative Model without Prior Distribution Matching

Variational Autoencoder (VAE) and its variations are classic generative models by learning a low-dimensional latent representation to satisfy some prior distribution (e.g., Gaussian distribution). Their advantages over GAN are that they can simultaneously generate high dimensional data and learn latent representations to reconstruct the inputs. However, it has been observed that a trade-off exists between reconstruction and generation since matching prior distribution may destroy the geometric structure of data manifold. To mitigate this problem, we propose to let the prior match the embedding distribution rather than imposing the latent variables to fit the prior. The embedding distribution is trained using a simple regularized autoencoder architecture which preserves the geometric structure to the maximum. Then an adversarial strategy is employed to achieve a latent mapping. We provide both theoretical and experimental support for the effectiveness of our method, which alleviates the contradiction between topological properties' preserving of data manifold and distribution matching in latent space.

Uniform Interpolation Constrained Geodesic Learning on Data Manifold

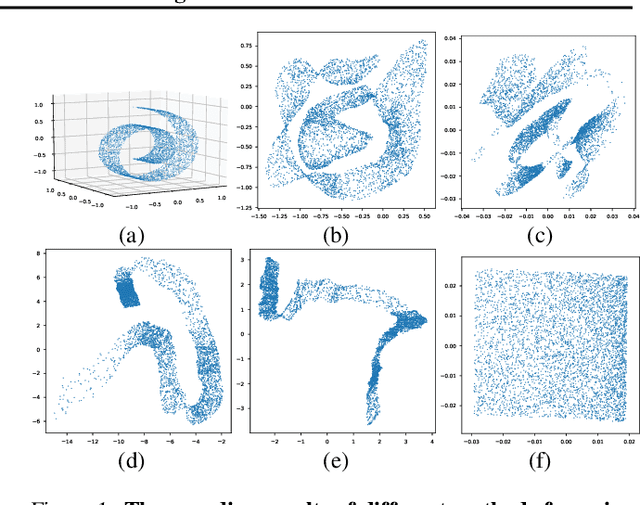
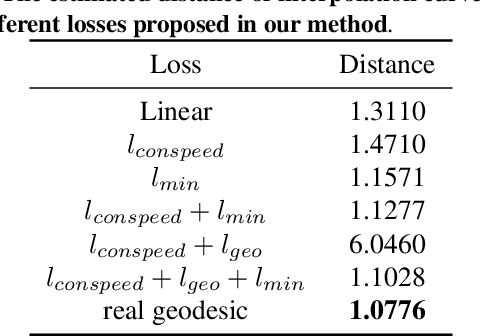
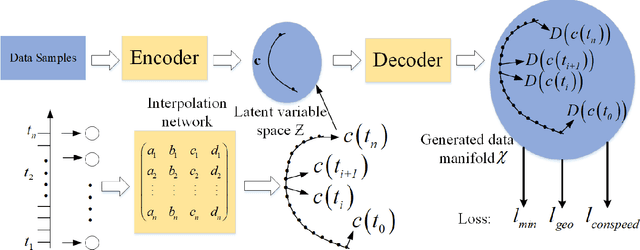
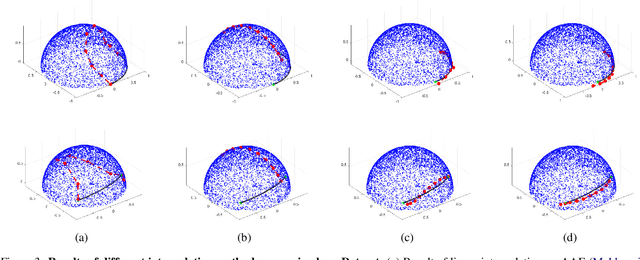
In this paper, we propose a method to learn a minimizing geodesic within a data manifold. Along the learned geodesic, our method can generate high-quality interpolations between two given data samples. Specifically, we use an autoencoder network to map data samples into latent space and perform interpolation via an interpolation network. We add prior geometric information to regularize our autoencoder for the convexity of representations so that for any given interpolation approach, the generated interpolations remain within the distribution of the data manifold. Before the learning of a geodesic, a proper Riemannianmetric should be defined. Therefore, we induce a Riemannian metric by the canonical metric in the Euclidean space which the data manifold is isometrically immersed in. Based on this defined Riemannian metric, we introduce a constant speed loss and a minimizing geodesic loss to regularize the interpolation network to generate uniform interpolation along the learned geodesic on the manifold. We provide a theoretical analysis of our model and use image translation as an example to demonstrate the effectiveness of our method.