Chu Chu
Uniform Interpolation Constrained Geodesic Learning on Data Manifold
Feb 28, 2020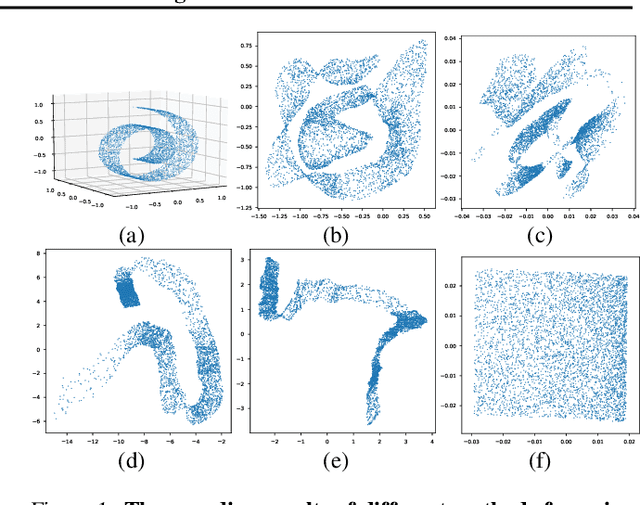
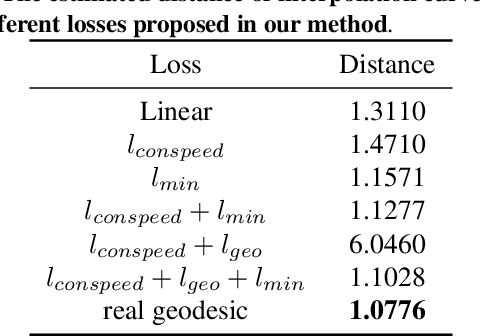
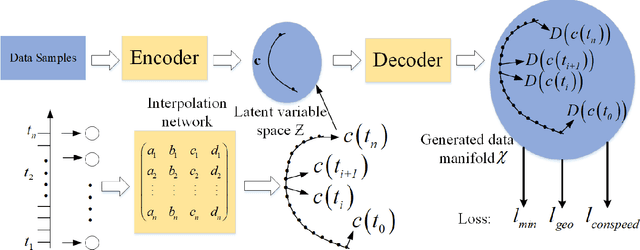
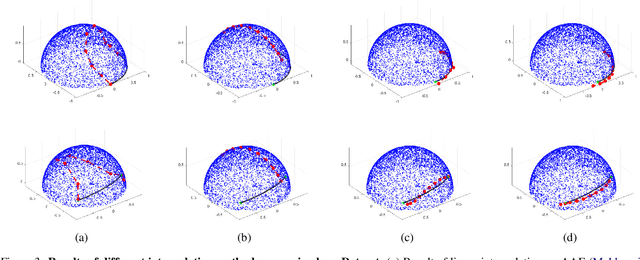
Abstract:In this paper, we propose a method to learn a minimizing geodesic within a data manifold. Along the learned geodesic, our method can generate high-quality interpolations between two given data samples. Specifically, we use an autoencoder network to map data samples into latent space and perform interpolation via an interpolation network. We add prior geometric information to regularize our autoencoder for the convexity of representations so that for any given interpolation approach, the generated interpolations remain within the distribution of the data manifold. Before the learning of a geodesic, a proper Riemannianmetric should be defined. Therefore, we induce a Riemannian metric by the canonical metric in the Euclidean space which the data manifold is isometrically immersed in. Based on this defined Riemannian metric, we introduce a constant speed loss and a minimizing geodesic loss to regularize the interpolation network to generate uniform interpolation along the learned geodesic on the manifold. We provide a theoretical analysis of our model and use image translation as an example to demonstrate the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge