Identifying metric structures of deep latent variable models

Deep latent variable models learn condensed representations of data that, hopefully, reflect the inner workings of the studied phenomena. Unfortunately, these latent representations are not statistically identifiable, meaning they cannot be uniquely determined. Domain experts, therefore, need to tread carefully when interpreting these. Current solutions limit the lack of identifiability through additional constraints on the latent variable model, e.g. by requiring labeled training data, or by restricting the expressivity of the model. We change the goal: instead of identifying the latent variables, we identify relationships between them such as meaningful distances, angles, and volumes. We prove this is feasible under very mild model conditions and without additional labeled data. We empirically demonstrate that our theory results in more reliable latent distances, offering a principled path forward in extracting trustworthy conclusions from deep latent variable models.

Distinguishing Cause from Effect with Causal Velocity Models

Bivariate structural causal models (SCM) are often used to infer causal direction by examining their goodness-of-fit under restricted model classes. In this paper, we describe a parametrization of bivariate SCMs in terms of a causal velocity by viewing the cause variable as time in a dynamical system. The velocity implicitly defines counterfactual curves via the solution of initial value problems where the observation specifies the initial condition. Using tools from measure transport, we obtain a unique correspondence between SCMs and the score function of the generated distribution via its causal velocity. Based on this, we derive an objective function that directly regresses the velocity against the score function, the latter of which can be estimated non-parametrically from observational data. We use this to develop a method for bivariate causal discovery that extends beyond known model classes such as additive or location scale noise, and that requires no assumptions on the noise distributions. When the score is estimated well, the objective is also useful for detecting model non-identifiability and misspecification. We present positive results in simulation and benchmark experiments where many existing methods fail, and perform ablation studies to examine the method's sensitivity to accurate score estimation.

Randomization Tests for Conditional Group Symmetry

Symmetry plays a central role in the sciences, machine learning, and statistics. While statistical tests for the presence of distributional invariance with respect to groups have a long history, tests for conditional symmetry in the form of equivariance or conditional invariance are absent from the literature. This work initiates the study of nonparametric randomization tests for symmetry (invariance or equivariance) of a conditional distribution under the action of a specified locally compact group. We develop a general framework for randomization tests with finite-sample Type I error control and, using kernel methods, implement tests with finite-sample power lower bounds. We also describe and implement approximate versions of the tests, which are asymptotically consistent. We study their properties empirically on synthetic examples, and on applications to testing for symmetry in two problems from high-energy particle physics.

Causal Inference with Cocycles

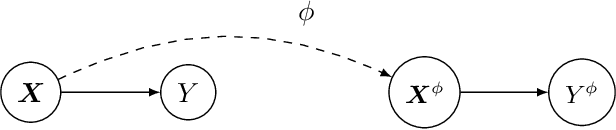
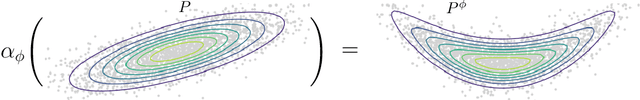
Many interventions in causal inference can be represented as transformations. We identify a local symmetry property satisfied by a large class of causal models under such interventions. Where present, this symmetry can be characterized by a type of map called a cocycle, an object that is central to dynamical systems theory. We show that such cocycles exist under general conditions and are sufficient to identify interventional and counterfactual distributions. We use these results to derive cocycle-based estimators for causal estimands and show they achieve semiparametric efficiency under typical conditions. Since (infinitely) many distributions can share the same cocycle, these estimators make causal inference robust to mis-specification by sidestepping superfluous modelling assumptions. We demonstrate both robustness and state-of-the-art performance in several simulations, and apply our method to estimate the effects of 401(k) pension plan eligibility on asset accumulation using a real dataset.

Mixed Variational Flows for Discrete Variables

Variational flows allow practitioners to learn complex continuous distributions, but approximating discrete distributions remains a challenge. Current methodologies typically embed the discrete target in a continuous space - usually via continuous relaxation or dequantization - and then apply a continuous flow. These approaches involve a surrogate target that may not capture the original discrete target, might have biased or unstable gradients, and can create a difficult optimization problem. In this work, we develop a variational flow family for discrete distributions without any continuous embedding. First, we develop a measure-preserving and discrete (MAD) invertible map that leaves the discrete target invariant, and then create a mixed variational flow (MAD Mix) based on that map. We also develop an extension to MAD Mix that handles joint discrete and continuous models. Our experiments suggest that MAD Mix produces more reliable approximations than continuous-embedding flows while being significantly faster to train.

Non-parametric Hypothesis Tests for Distributional Group Symmetry

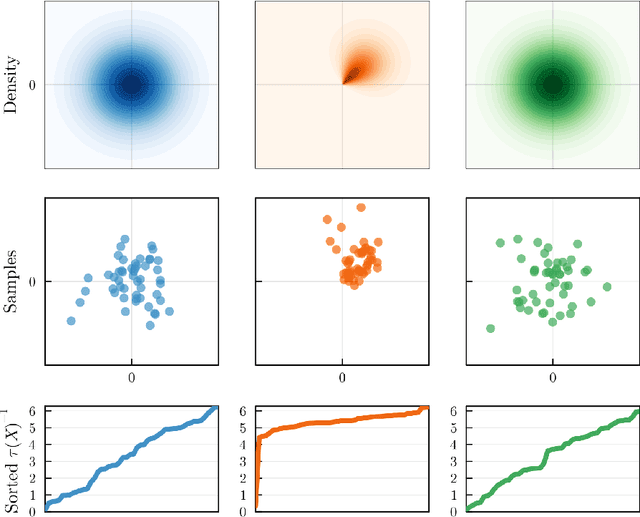
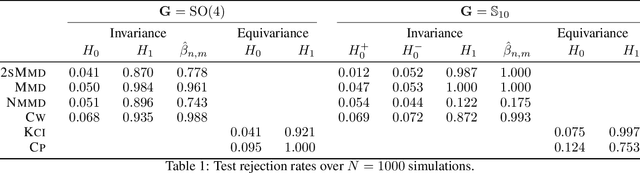
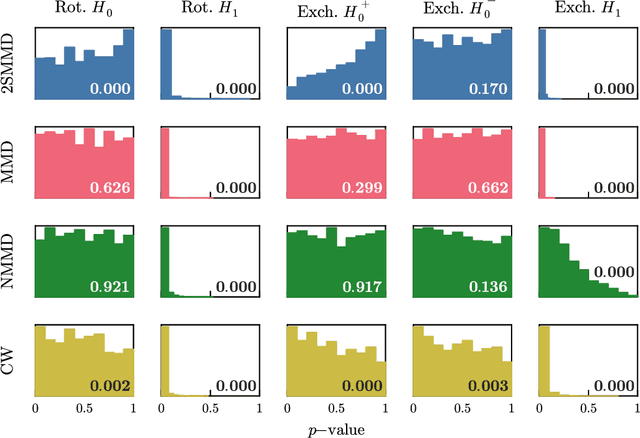
Symmetry plays a central role in the sciences, machine learning, and statistics. For situations in which data are known to obey a symmetry, a multitude of methods that exploit symmetry have been developed. Statistical tests for the presence or absence of general group symmetry, however, are largely non-existent. This work formulates non-parametric hypothesis tests, based on a single independent and identically distributed sample, for distributional symmetry under a specified group. We provide a general formulation of tests for symmetry that apply to two broad settings. The first setting tests for the invariance of a marginal or joint distribution under the action of a compact group. Here, an asymptotically unbiased test only requires a computable metric on the space of probability distributions and the ability to sample uniformly random group elements. Building on this, we propose an easy-to-implement conditional Monte Carlo test and prove that it achieves exact $p$-values with finitely many observations and Monte Carlo samples. The second setting tests for the invariance or equivariance of a conditional distribution under the action of a locally compact group. We show that the test for conditional invariance or equivariance can be formulated as particular tests of conditional independence. We implement these tests from both settings using kernel methods and study them empirically on synthetic data. Finally, we apply them to testing for symmetry in geomagnetic satellite data and in two problems from high-energy particle physics.

Indeterminacy in Latent Variable Models: Characterization and Strong Identifiability

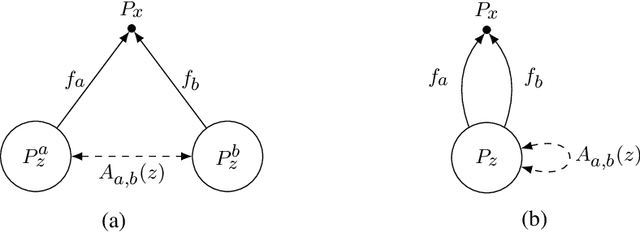
Most modern latent variable and probabilistic generative models, such as the variational autoencoder (VAE), have certain indeterminacies that are unresolvable even with an infinite amount of data. Recent applications of such models have indicated the need for \textit{strongly} identifiable models, in which an observation corresponds to a unique latent code. Progress has been made towards reducing model indeterminacies while maintaining flexibility, most notably by the iVAE (arXiv:1907.04809 [stat.ML]), which excludes many -- but not all -- indeterminacies. We construct a full theoretical framework for analyzing the indeterminacies of latent variable models, and characterize them precisely in terms of properties of the generator functions and the latent variable prior distributions. To illustrate, we apply the framework to better understand the structure of recent identifiability results. We then investigate how we might specify strongly identifiable latent variable models, and construct two such classes of models. One is a straightforward modification of iVAE; the other uses ideas from optimal transport and leads to novel models and connections to recent work.

Lossy Compression for Lossless Prediction

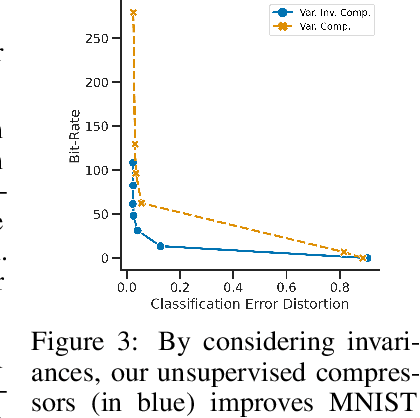
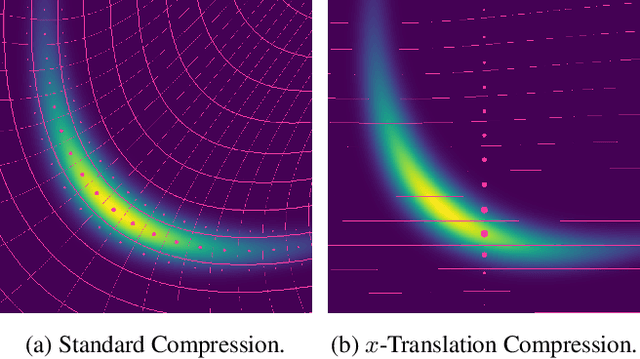
Most data is automatically collected and only ever "seen" by algorithms. Yet, data compressors preserve perceptual fidelity rather than just the information needed by algorithms performing downstream tasks. In this paper, we characterize the bit-rate required to ensure high performance on all predictive tasks that are invariant under a set of transformations, such as data augmentations. Based on our theory, we design unsupervised objectives for training neural compressors. Using these objectives, we train a generic image compressor that achieves substantial rate savings (more than $1000\times$ on ImageNet) compared to JPEG on 8 datasets, without decreasing downstream classification performance.

Uncertainty in Neural Processes

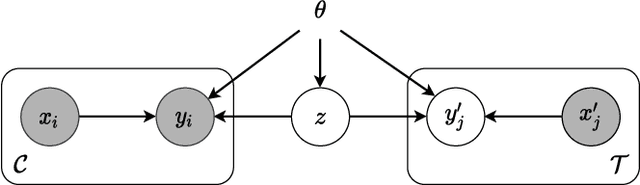
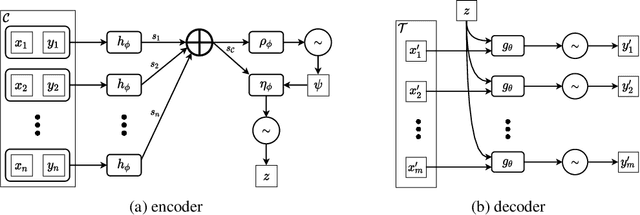
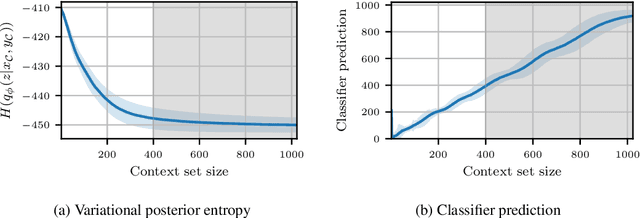
We explore the effects of architecture and training objective choice on amortized posterior predictive inference in probabilistic conditional generative models. We aim this work to be a counterpoint to a recent trend in the literature that stresses achieving good samples when the amount of conditioning data is large. We instead focus our attention on the case where the amount of conditioning data is small. We highlight specific architecture and objective choices that we find lead to qualitative and quantitative improvement to posterior inference in this low data regime. Specifically we explore the effects of choices of pooling operator and variational family on posterior quality in neural processes. Superior posterior predictive samples drawn from our novel neural process architectures are demonstrated via image completion/in-painting experiments.

On the Benefits of Invariance in Neural Networks

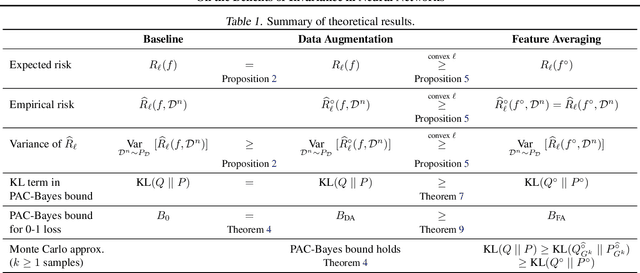
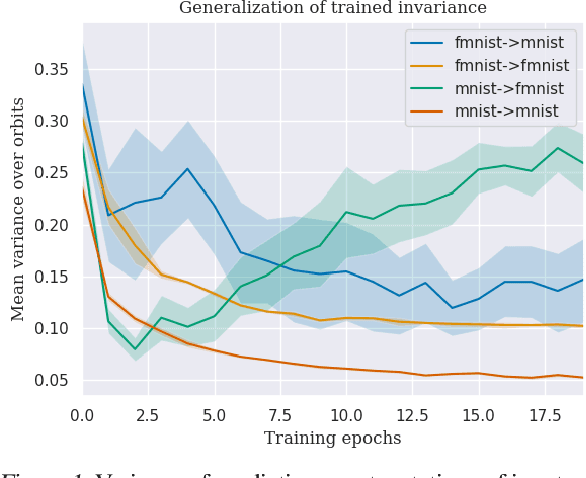
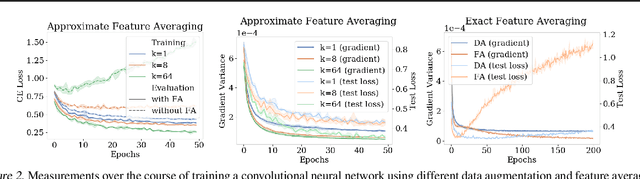
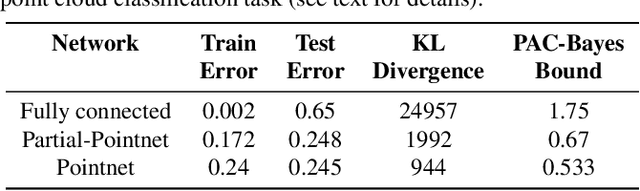
Many real world data analysis problems exhibit invariant structure, and models that take advantage of this structure have shown impressive empirical performance, particularly in deep learning. While the literature contains a variety of methods to incorporate invariance into models, theoretical understanding is poor and there is no way to assess when one method should be preferred over another. In this work, we analyze the benefits and limitations of two widely used approaches in deep learning in the presence of invariance: data augmentation and feature averaging. We prove that training with data augmentation leads to better estimates of risk and gradients thereof, and we provide a PAC-Bayes generalization bound for models trained with data augmentation. We also show that compared to data augmentation, feature averaging reduces generalization error when used with convex losses, and tightens PAC-Bayes bounds. We provide empirical support of these theoretical results, including a demonstration of why generalization may not improve by training with data augmentation: the `learned invariance' fails outside of the training distribution.