Distinguishing Cause from Effect with Causal Velocity Models

Bivariate structural causal models (SCM) are often used to infer causal direction by examining their goodness-of-fit under restricted model classes. In this paper, we describe a parametrization of bivariate SCMs in terms of a causal velocity by viewing the cause variable as time in a dynamical system. The velocity implicitly defines counterfactual curves via the solution of initial value problems where the observation specifies the initial condition. Using tools from measure transport, we obtain a unique correspondence between SCMs and the score function of the generated distribution via its causal velocity. Based on this, we derive an objective function that directly regresses the velocity against the score function, the latter of which can be estimated non-parametrically from observational data. We use this to develop a method for bivariate causal discovery that extends beyond known model classes such as additive or location scale noise, and that requires no assumptions on the noise distributions. When the score is estimated well, the objective is also useful for detecting model non-identifiability and misspecification. We present positive results in simulation and benchmark experiments where many existing methods fail, and perform ablation studies to examine the method's sensitivity to accurate score estimation.

Spectral Representations for Accurate Causal Uncertainty Quantification with Gaussian Processes

Accurate uncertainty quantification for causal effects is essential for robust decision making in complex systems, but remains challenging in non-parametric settings. One promising framework represents conditional distributions in a reproducing kernel Hilbert space and places Gaussian process priors on them to infer posteriors on causal effects, but requires restrictive nuclear dominant kernels and approximations that lead to unreliable uncertainty estimates. In this work, we introduce a method, IMPspec, that addresses these limitations via a spectral representation of the Hilbert space. We show that posteriors in this model can be obtained explicitly, by extending a result in Hilbert space regression theory. We also learn the spectral representation to optimise posterior calibration. Our method achieves state-of-the-art performance in uncertainty quantification and causal Bayesian optimisation across simulations and a healthcare application.

Causal Inference with Cocycles

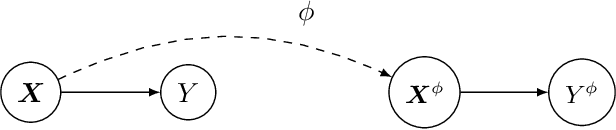
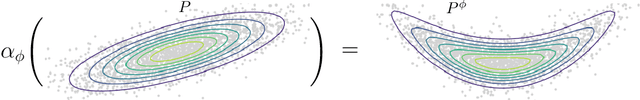
Many interventions in causal inference can be represented as transformations. We identify a local symmetry property satisfied by a large class of causal models under such interventions. Where present, this symmetry can be characterized by a type of map called a cocycle, an object that is central to dynamical systems theory. We show that such cocycles exist under general conditions and are sufficient to identify interventional and counterfactual distributions. We use these results to derive cocycle-based estimators for causal estimands and show they achieve semiparametric efficiency under typical conditions. Since (infinitely) many distributions can share the same cocycle, these estimators make causal inference robust to mis-specification by sidestepping superfluous modelling assumptions. We demonstrate both robustness and state-of-the-art performance in several simulations, and apply our method to estimate the effects of 401(k) pension plan eligibility on asset accumulation using a real dataset.

Fast and Scalable Spike and Slab Variable Selection in High-Dimensional Gaussian Processes

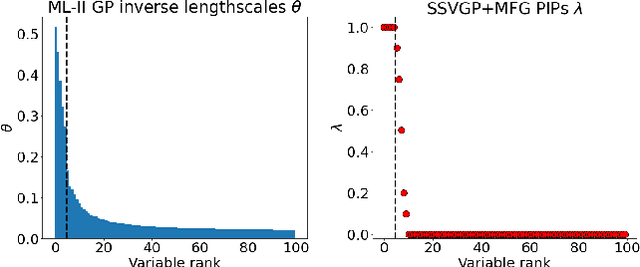
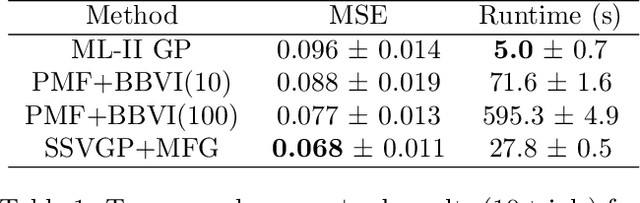
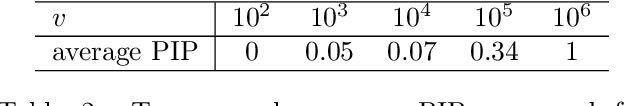
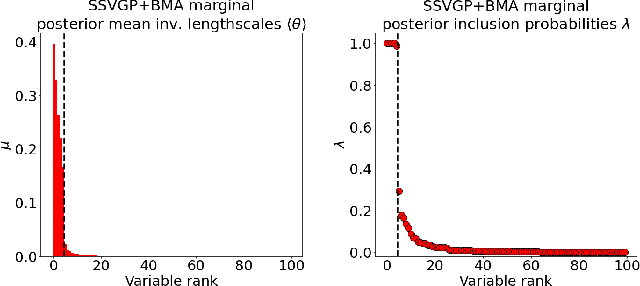
Variable selection in Gaussian processes (GPs) is typically undertaken by thresholding the inverse lengthscales of `automatic relevance determination' kernels, but in high-dimensional datasets this approach can be unreliable. A more probabilistically principled alternative is to use spike and slab priors and infer a posterior probability of variable inclusion. However, existing implementations in GPs are extremely costly to run in both high-dimensional and large-$n$ datasets, or are intractable for most kernels. As such, we develop a fast and scalable variational inference algorithm for the spike and slab GP that is tractable with arbitrary differentiable kernels. We improve our algorithm's ability to adapt to the sparsity of relevant variables by Bayesian model averaging over hyperparameters, and achieve substantial speed ups using zero temperature posterior restrictions, dropout pruning and nearest neighbour minibatching. In experiments our method consistently outperforms vanilla and sparse variational GPs whilst retaining similar runtimes (even when $n=10^6$) and performs competitively with a spike and slab GP using MCMC but runs up to $1000$ times faster.