Peter Orbanz
A Single Architecture for Representing Invariance Under Any Space Group
Dec 16, 2025Abstract:Incorporating known symmetries in data into machine learning models has consistently improved predictive accuracy, robustness, and generalization. However, achieving exact invariance to specific symmetries typically requires designing bespoke architectures for each group of symmetries, limiting scalability and preventing knowledge transfer across related symmetries. In the case of the space groups, symmetries critical to modeling crystalline solids in materials science and condensed matter physics, this challenge is particularly salient as there are 230 such groups in three dimensions. In this work we present a new approach to such crystallographic symmetries by developing a single machine learning architecture that is capable of adapting its weights automatically to enforce invariance to any input space group. Our approach is based on constructing symmetry-adapted Fourier bases through an explicit characterization of constraints that group operations impose on Fourier coefficients. Encoding these constraints into a neural network layer enables weight sharing across different space groups, allowing the model to leverage structural similarities between groups and overcome data sparsity when limited measurements are available for specific groups. We demonstrate the effectiveness of this approach in achieving competitive performance on material property prediction tasks and performing zero-shot learning to generalize to unseen groups.
Distinguishing Cause from Effect with Causal Velocity Models
Feb 07, 2025



Abstract:Bivariate structural causal models (SCM) are often used to infer causal direction by examining their goodness-of-fit under restricted model classes. In this paper, we describe a parametrization of bivariate SCMs in terms of a causal velocity by viewing the cause variable as time in a dynamical system. The velocity implicitly defines counterfactual curves via the solution of initial value problems where the observation specifies the initial condition. Using tools from measure transport, we obtain a unique correspondence between SCMs and the score function of the generated distribution via its causal velocity. Based on this, we derive an objective function that directly regresses the velocity against the score function, the latter of which can be estimated non-parametrically from observational data. We use this to develop a method for bivariate causal discovery that extends beyond known model classes such as additive or location scale noise, and that requires no assumptions on the noise distributions. When the score is estimated well, the objective is also useful for detecting model non-identifiability and misspecification. We present positive results in simulation and benchmark experiments where many existing methods fail, and perform ablation studies to examine the method's sensitivity to accurate score estimation.
Diagonal Symmetrization of Neural Network Solvers for the Many-Electron Schrödinger Equation
Feb 07, 2025Abstract:Incorporating group symmetries into neural networks has been a cornerstone of success in many AI-for-science applications. Diagonal groups of isometries, which describe the invariance under a simultaneous movement of multiple objects, arise naturally in many-body quantum problems. Despite their importance, diagonal groups have received relatively little attention, as they lack a natural choice of invariant maps except in special cases. We study different ways of incorporating diagonal invariance in neural network ans\"atze trained via variational Monte Carlo methods, and consider specifically data augmentation, group averaging and canonicalization. We show that, contrary to standard ML setups, in-training symmetrization destabilizes training and can lead to worse performance. Our theoretical and numerical results indicate that this unexpected behavior may arise from a unique computational-statistical tradeoff not found in standard ML analyses of symmetrization. Meanwhile, we demonstrate that post hoc averaging is less sensitive to such tradeoffs and emerges as a simple, flexible and effective method for improving neural network solvers.
Spectral Representations for Accurate Causal Uncertainty Quantification with Gaussian Processes
Oct 18, 2024Abstract:Accurate uncertainty quantification for causal effects is essential for robust decision making in complex systems, but remains challenging in non-parametric settings. One promising framework represents conditional distributions in a reproducing kernel Hilbert space and places Gaussian process priors on them to infer posteriors on causal effects, but requires restrictive nuclear dominant kernels and approximations that lead to unreliable uncertainty estimates. In this work, we introduce a method, IMPspec, that addresses these limitations via a spectral representation of the Hilbert space. We show that posteriors in this model can be obtained explicitly, by extending a result in Hilbert space regression theory. We also learn the spectral representation to optimise posterior calibration. Our method achieves state-of-the-art performance in uncertainty quantification and causal Bayesian optimisation across simulations and a healthcare application.
Global optimality under amenable symmetry constraints
Feb 12, 2024
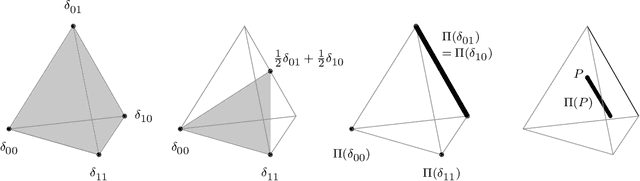
Abstract:We ask whether there exists a function or measure that (1) minimizes a given convex functional or risk and (2) satisfies a symmetry property specified by an amenable group of transformations. Examples of such symmetry properties are invariance, equivariance, or quasi-invariance. Our results draw on old ideas of Stein and Le Cam and on approximate group averages that appear in ergodic theorems for amenable groups. A class of convex sets known as orbitopes in convex analysis emerges as crucial, and we establish properties of such orbitopes in nonparametric settings. We also show how a simple device called a cocycle can be used to reduce different forms of symmetry to a single problem. As applications, we obtain results on invariant kernel mean embeddings and a Monge-Kantorovich theorem on optimality of transport plans under symmetry constraints. We also explain connections to the Hunt-Stein theorem on invariant tests.
Representing and Learning Functions Invariant Under Crystallographic Groups
Jun 08, 2023Abstract:Crystallographic groups describe the symmetries of crystals and other repetitive structures encountered in nature and the sciences. These groups include the wallpaper and space groups. We derive linear and nonlinear representations of functions that are (1) smooth and (2) invariant under such a group. The linear representation generalizes the Fourier basis to crystallographically invariant basis functions. We show that such a basis exists for each crystallographic group, that it is orthonormal in the relevant $L_2$ space, and recover the standard Fourier basis as a special case for pure shift groups. The nonlinear representation embeds the orbit space of the group into a finite-dimensional Euclidean space. We show that such an embedding exists for every crystallographic group, and that it factors functions through a generalization of a manifold called an orbifold. We describe algorithms that, given a standardized description of the group, compute the Fourier basis and an embedding map. As examples, we construct crystallographically invariant neural networks, kernel machines, and Gaussian processes.
Quantifying the Effects of Data Augmentation
Feb 18, 2022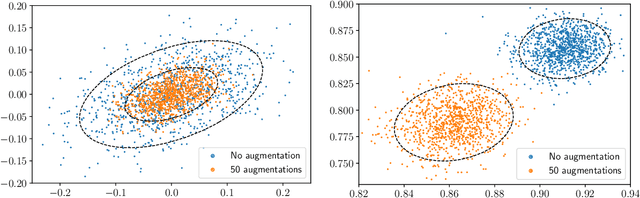
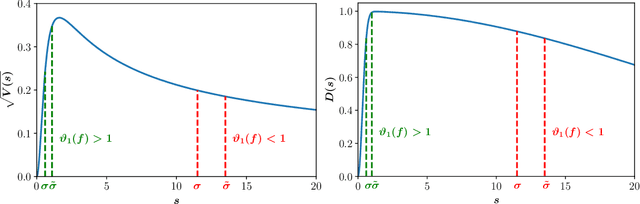
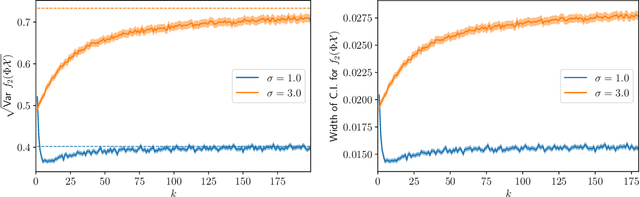
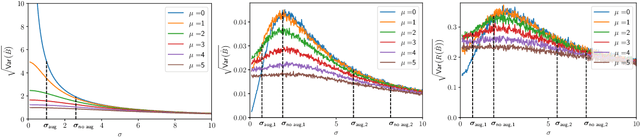
Abstract:We provide results that exactly quantify how data augmentation affects the convergence rate and variance of estimates. They lead to some unexpected findings: Contrary to common intuition, data augmentation may increase rather than decrease uncertainty of estimates, such as the empirical prediction risk. Our main theoretical tool is a limit theorem for functions of randomly transformed, high-dimensional random vectors. The proof draws on work in probability on noise stability of functions of many variables. The pathological behavior we identify is not a consequence of complex models, but can occur even in the simplest settings -- one of our examples is a linear ridge regressor with two parameters. On the other hand, our results also show that data augmentation can have real, quantifiable benefits.
Random Walk Models of Network Formation and Sequential Monte Carlo Methods for Graphs
Jul 07, 2018
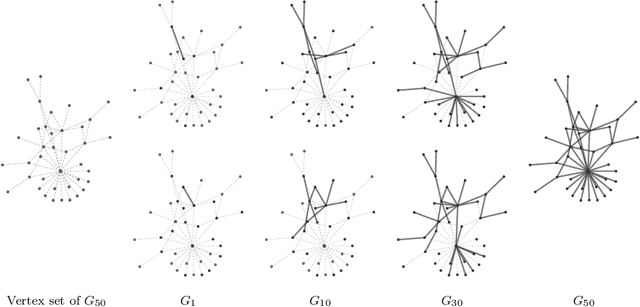

Abstract:We introduce a class of generative network models that insert edges by connecting the starting and terminal vertices of a random walk on the network graph. Within the taxonomy of statistical network models, this class is distinguished by permitting the location of a new edge to explicitly depend on the structure of the graph, but being nonetheless statistically and computationally tractable. In the limit of infinite walk length, the model converges to an extension of the preferential attachment model---in this sense, it can be motivated alternatively by asking what preferential attachment is an approximation to. Theoretical properties, including the limiting degree sequence, are studied analytically. If the entire history of the graph is observed, parameters can be estimated by maximum likelihood. If only the final graph is available, its history can be imputed using MCMC. We develop a class of sequential Monte Carlo algorithms that are more generally applicable to sequential network models, and may be of interest in their own right. The model parameters can be recovered from a single graph generated by the model. Applications to data clarify the role of the random walk length as a length scale of interactions within the graph.
Empirical Risk Minimization and Stochastic Gradient Descent for Relational Data
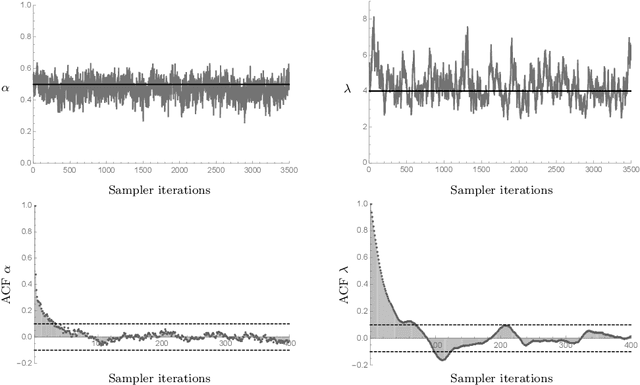
Jun 27, 2018


Abstract:Empirical risk minimization is the principal tool for prediction problems, but its extension to relational data remains unsolved. We solve this problem using recent advances in graph sampling theory. We (i) define an empirical risk for relational data and (ii) obtain stochastic gradients for this risk that are automatically unbiased. The key ingredient is to consider the method by which data is sampled from a graph as an explicit component of model design. Theoretical results establish that the choice of sampling scheme is critical. By integrating fast implementations of graph sampling schemes with standard automatic differentiation tools, we are able to solve the risk minimization in a plug-and-play fashion even on large datasets. We demonstrate empirically that relational ERM models achieve state-of-the-art results on semi-supervised node classification tasks. The experiments also confirm the importance of the choice of sampling scheme.
Compressibility and Generalization in Large-Scale Deep Learning
May 21, 2018
Abstract:Modern neural networks are highly overparameterized, with capacity to substantially overfit to training data. Nevertheless, these networks often generalize well in practice. It has also been observed that trained networks can often be "compressed" to much smaller representations. The purpose of this paper is to connect these two empirical observations. Our main technical result is a generalization bound for compressed networks based on the compressed size. Combined with off-the-shelf compression algorithms, the bound leads to state of the art generalization guarantees; in particular, we provide the first non-vacuous generalization guarantees for realistic architectures applied to the ImageNet classification problem. As additional evidence connecting compression and generalization, we show that compressibility of models that tend to overfit is limited: We establish an absolute limit on expected compressibility as a function of expected generalization error, where the expectations are over the random choice of training examples. The bounds are complemented by empirical results that show an increase in overfitting implies an increase in the number of bits required to describe a trained network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge