Random Walk Models of Network Formation and Sequential Monte Carlo Methods for Graphs
Paper and Code
Jul 07, 2018
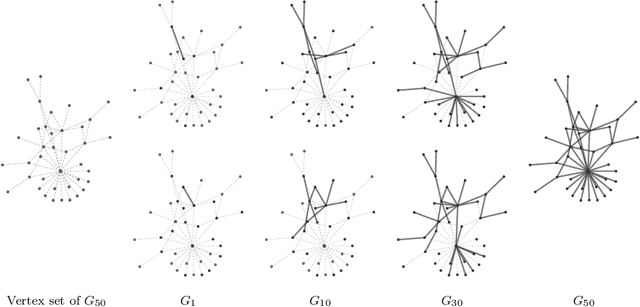

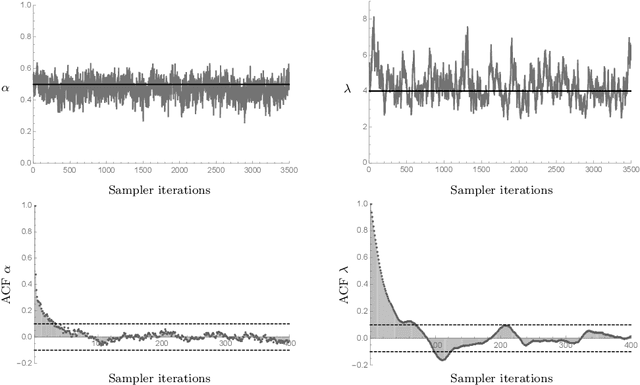
We introduce a class of generative network models that insert edges by connecting the starting and terminal vertices of a random walk on the network graph. Within the taxonomy of statistical network models, this class is distinguished by permitting the location of a new edge to explicitly depend on the structure of the graph, but being nonetheless statistically and computationally tractable. In the limit of infinite walk length, the model converges to an extension of the preferential attachment model---in this sense, it can be motivated alternatively by asking what preferential attachment is an approximation to. Theoretical properties, including the limiting degree sequence, are studied analytically. If the entire history of the graph is observed, parameters can be estimated by maximum likelihood. If only the final graph is available, its history can be imputed using MCMC. We develop a class of sequential Monte Carlo algorithms that are more generally applicable to sequential network models, and may be of interest in their own right. The model parameters can be recovered from a single graph generated by the model. Applications to data clarify the role of the random walk length as a length scale of interactions within the graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge