Bayesian Models of Graphs, Arrays and Other Exchangeable Random Structures
Paper and Code
Feb 13, 2015
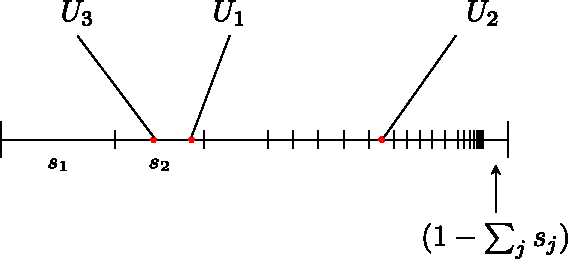
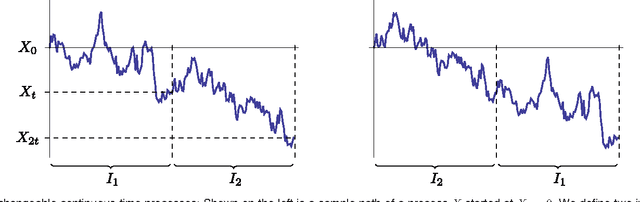

The natural habitat of most Bayesian methods is data represented by exchangeable sequences of observations, for which de Finetti's theorem provides the theoretical foundation. Dirichlet process clustering, Gaussian process regression, and many other parametric and nonparametric Bayesian models fall within the remit of this framework; many problems arising in modern data analysis do not. This article provides an introduction to Bayesian models of graphs, matrices, and other data that can be modeled by random structures. We describe results in probability theory that generalize de Finetti's theorem to such data and discuss their relevance to nonparametric Bayesian modeling. With the basic ideas in place, we survey example models available in the literature; applications of such models include collaborative filtering, link prediction, and graph and network analysis. We also highlight connections to recent developments in graph theory and probability, and sketch the more general mathematical foundation of Bayesian methods for other types of data beyond sequences and arrays.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge