Empirical Risk Minimization and Stochastic Gradient Descent for Relational Data

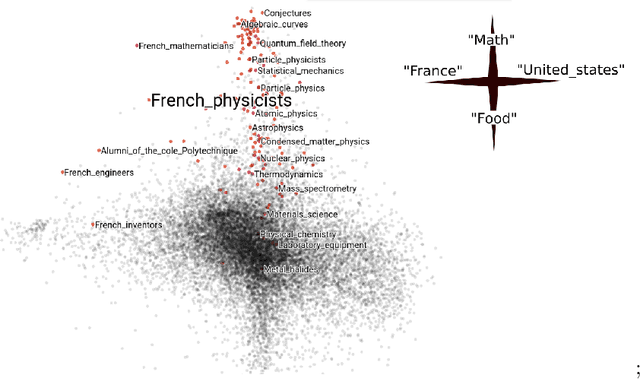
Empirical risk minimization is the principal tool for prediction problems, but its extension to relational data remains unsolved. We solve this problem using recent advances in graph sampling theory. We (i) define an empirical risk for relational data and (ii) obtain stochastic gradients for this risk that are automatically unbiased. The key ingredient is to consider the method by which data is sampled from a graph as an explicit component of model design. Theoretical results establish that the choice of sampling scheme is critical. By integrating fast implementations of graph sampling schemes with standard automatic differentiation tools, we are able to solve the risk minimization in a plug-and-play fashion even on large datasets. We demonstrate empirically that relational ERM models achieve state-of-the-art results on semi-supervised node classification tasks. The experiments also confirm the importance of the choice of sampling scheme.