Morgane Austern
Graph Attention Network for Node Regression on Random Geometric Graphs with Erdős--Rényi contamination
Jan 30, 2026Abstract:Graph attention networks (GATs) are widely used and often appear robust to noise in node covariates and edges, yet rigorous statistical guarantees demonstrating a provable advantage of GATs over non-attention graph neural networks~(GNNs) are scarce. We partially address this gap for node regression with graph-based errors-in-variables models under simultaneous covariate and edge corruption: responses are generated from latent node-level covariates, but only noise-perturbed versions of the latent covariates are observed; and the sample graph is a random geometric graph created from the node covariates but contaminated by independent Erdős--Rényi edges. We propose and analyze a carefully designed, task-specific GAT that constructs denoised proxy features for regression. We prove that regressing the response variables on the proxies achieves lower error asymptotically in (a) estimating the regression coefficient compared to the ordinary least squares (OLS) estimator on the noisy node covariates, and (b) predicting the response for an unlabelled node compared to a vanilla graph convolutional network~(GCN) -- under mild growth conditions. Our analysis leverages high-dimensional geometric tail bounds and concentration for neighbourhood counts and sample covariances. We verify our theoretical findings through experiments on synthetically generated data. We also perform experiments on real-world graphs and demonstrate the effectiveness of the attention mechanism in several node regression tasks.
Inference on Optimal Policy Values and Other Irregular Functionals via Smoothing
Jul 15, 2025Abstract:Constructing confidence intervals for the value of an optimal treatment policy is an important problem in causal inference. Insight into the optimal policy value can guide the development of reward-maximizing, individualized treatment regimes. However, because the functional that defines the optimal value is non-differentiable, standard semi-parametric approaches for performing inference fail to be directly applicable. Existing approaches for handling this non-differentiability fall roughly into two camps. In one camp are estimators based on constructing smooth approximations of the optimal value. These approaches are computationally lightweight, but typically place unrealistic parametric assumptions on outcome regressions. In another camp are approaches that directly de-bias the non-smooth objective. These approaches don't place parametric assumptions on nuisance functions, but they either require the computation of intractably-many nuisance estimates, assume unrealistic $L^\infty$ nuisance convergence rates, or make strong margin assumptions that prohibit non-response to a treatment. In this paper, we revisit the problem of constructing smooth approximations of non-differentiable functionals. By carefully controlling first-order bias and second-order remainders, we show that a softmax smoothing-based estimator can be used to estimate parameters that are specified as a maximum of scores involving nuisance components. In particular, this includes the value of the optimal treatment policy as a special case. Our estimator obtains $\sqrt{n}$ convergence rates, avoids parametric restrictions/unrealistic margin assumptions, and is often statistically efficient.
Random Geometric Graph Alignment with Graph Neural Networks
Feb 12, 2024Abstract:We characterize the performance of graph neural networks for graph alignment problems in the presence of vertex feature information. More specifically, given two graphs that are independent perturbations of a single random geometric graph with noisy sparse features, the task is to recover an unknown one-to-one mapping between the vertices of the two graphs. We show under certain conditions on the sparsity and noise level of the feature vectors, a carefully designed one-layer graph neural network can with high probability recover the correct alignment between the vertices with the help of the graph structure. We also prove that our conditions on the noise level are tight up to logarithmic factors. Finally we compare the performance of the graph neural network to directly solving an assignment problem on the noisy vertex features. We demonstrate that when the noise level is at least constant this direct matching fails to have perfect recovery while the graph neural network can tolerate noise level growing as fast as a power of the size of the graph.
Statistical Guarantees for Link Prediction using Graph Neural Networks
Feb 07, 2024Abstract:This paper derives statistical guarantees for the performance of Graph Neural Networks (GNNs) in link prediction tasks on graphs generated by a graphon. We propose a linear GNN architecture (LG-GNN) that produces consistent estimators for the underlying edge probabilities. We establish a bound on the mean squared error and give guarantees on the ability of LG-GNN to detect high-probability edges. Our guarantees hold for both sparse and dense graphs. Finally, we demonstrate some of the shortcomings of the classical GCN architecture, as well as verify our results on real and synthetic datasets.
Inference on Optimal Dynamic Policies via Softmax Approximation
Mar 08, 2023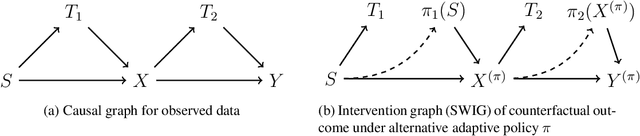

Abstract:Estimating optimal dynamic policies from offline data is a fundamental problem in dynamic decision making. In the context of causal inference, the problem is known as estimating the optimal dynamic treatment regime. Even though there exists a plethora of methods for estimation, constructing confidence intervals for the value of the optimal regime and structural parameters associated with it is inherently harder, as it involves non-linear and non-differentiable functionals of un-known quantities that need to be estimated. Prior work resorted to sub-sample approaches that can deteriorate the quality of the estimate. We show that a simple soft-max approximation to the optimal treatment regime, for an appropriately fast growing temperature parameter, can achieve valid inference on the truly optimal regime. We illustrate our result for a two-period optimal dynamic regime, though our approach should directly extend to the finite horizon case. Our work combines techniques from semi-parametric inference and $g$-estimation, together with an appropriate triangular array central limit theorem, as well as a novel analysis of the asymptotic influence and asymptotic bias of softmax approximations.
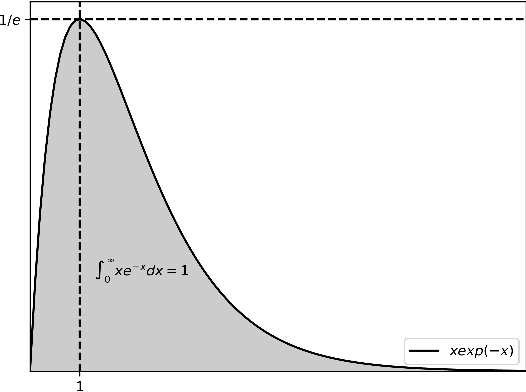
Debiased Machine Learning without Sample-Splitting for Stable Estimators
Jun 03, 2022
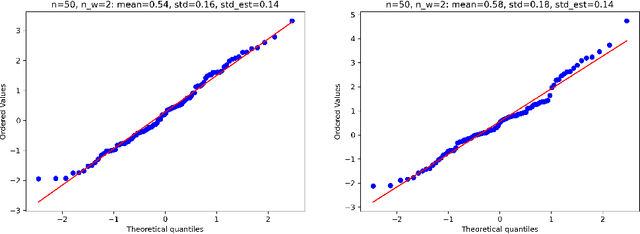
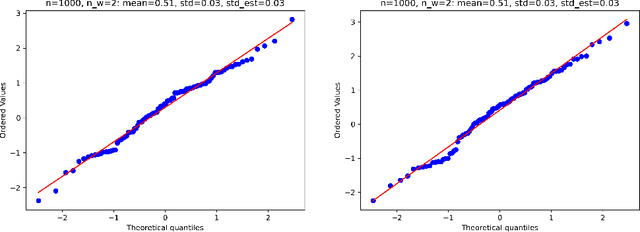
Abstract:Estimation and inference on causal parameters is typically reduced to a generalized method of moments problem, which involves auxiliary functions that correspond to solutions to a regression or classification problem. Recent line of work on debiased machine learning shows how one can use generic machine learning estimators for these auxiliary problems, while maintaining asymptotic normality and root-$n$ consistency of the target parameter of interest, while only requiring mean-squared-error guarantees from the auxiliary estimation algorithms. The literature typically requires that these auxiliary problems are fitted on a separate sample or in a cross-fitting manner. We show that when these auxiliary estimation algorithms satisfy natural leave-one-out stability properties, then sample splitting is not required. This allows for sample re-use, which can be beneficial in moderately sized sample regimes. For instance, we show that the stability properties that we propose are satisfied for ensemble bagged estimators, built via sub-sampling without replacement, a popular technique in machine learning practice.
Quantifying the Effects of Data Augmentation
Feb 18, 2022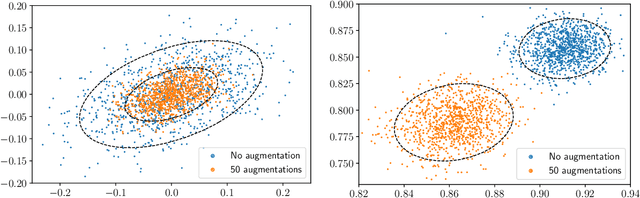
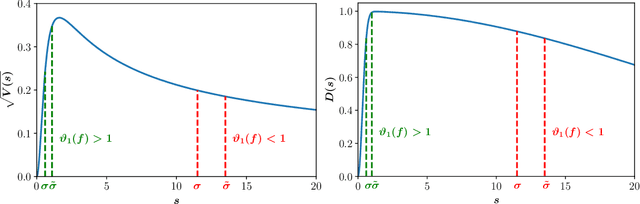
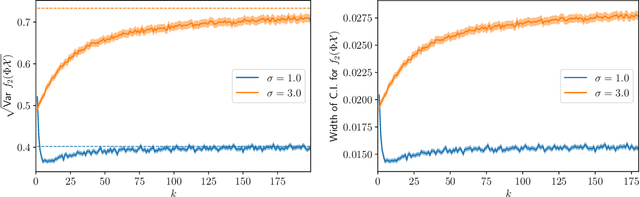
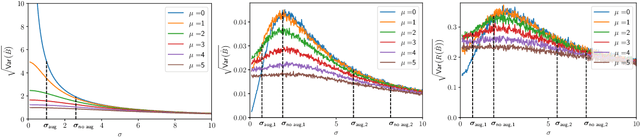
Abstract:We provide results that exactly quantify how data augmentation affects the convergence rate and variance of estimates. They lead to some unexpected findings: Contrary to common intuition, data augmentation may increase rather than decrease uncertainty of estimates, such as the empirical prediction risk. Our main theoretical tool is a limit theorem for functions of randomly transformed, high-dimensional random vectors. The proof draws on work in probability on noise stability of functions of many variables. The pathological behavior we identify is not a consequence of complex models, but can occur even in the simplest settings -- one of our examples is a linear ridge regressor with two parameters. On the other hand, our results also show that data augmentation can have real, quantifiable benefits.
Asymptotics of Network Embeddings Learned via Subsampling
Jul 06, 2021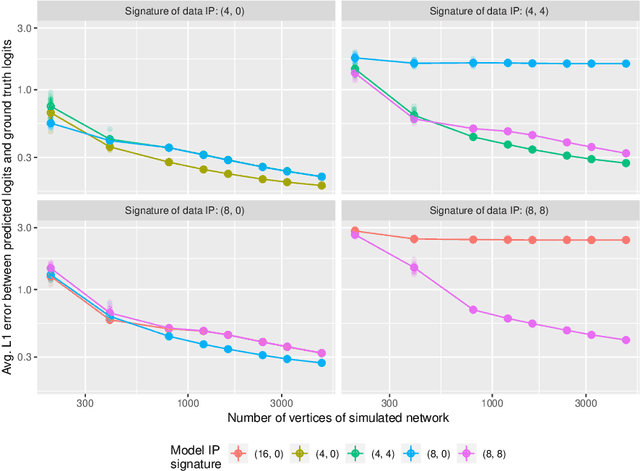
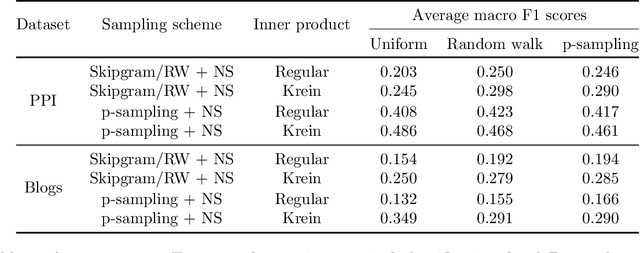
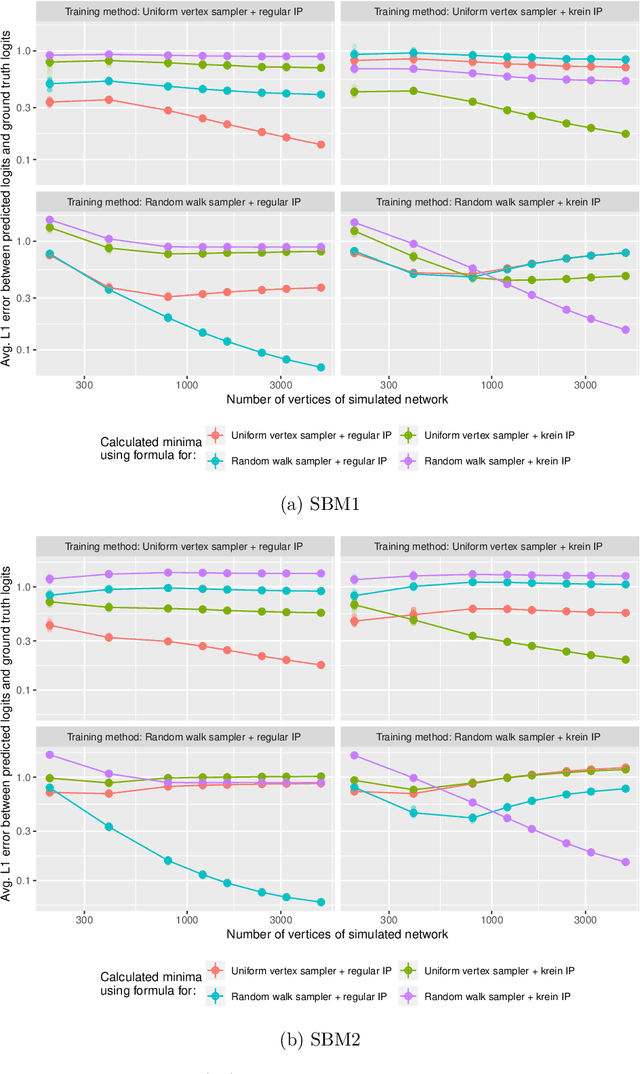
Abstract:Network data are ubiquitous in modern machine learning, with tasks of interest including node classification, node clustering and link prediction. A frequent approach begins by learning an Euclidean embedding of the network, to which algorithms developed for vector-valued data are applied. For large networks, embeddings are learned using stochastic gradient methods where the sub-sampling scheme can be freely chosen. Despite the strong empirical performance of such methods, they are not well understood theoretically. Our work encapsulates representation methods using a subsampling approach, such as node2vec, into a single unifying framework. We prove, under the assumption that the graph is exchangeable, that the distribution of the learned embedding vectors asymptotically decouples. Moreover, we characterize the asymptotic distribution and provided rates of convergence, in terms of the latent parameters, which includes the choice of loss function and the embedding dimension. This provides a theoretical foundation to understand what the embedding vectors represent and how well these methods perform on downstream tasks. Notably, we observe that typically used loss functions may lead to shortcomings, such as a lack of Fisher consistency.
Asymptotics of the Empirical Bootstrap Method Beyond Asymptotic Normality
Nov 23, 2020Abstract:One of the most commonly used methods for forming confidence intervals for statistical inference is the empirical bootstrap, which is especially expedient when the limiting distribution of the estimator is unknown. However, despite its ubiquitous role, its theoretical properties are still not well understood for non-asymptotically normal estimators. In this paper, under stability conditions, we establish the limiting distribution of the empirical bootstrap estimator, derive tight conditions for it to be asymptotically consistent, and quantify the speed of convergence. Moreover, we propose three alternative ways to use the bootstrap method to build confidence intervals with coverage guarantees. Finally, we illustrate the generality and tightness of our results by a series of examples, including uniform confidence bands, two-sample kernel tests, minmax stochastic programs and the empirical risk of stacked estimators.
Empirical Risk Minimization and Stochastic Gradient Descent for Relational Data
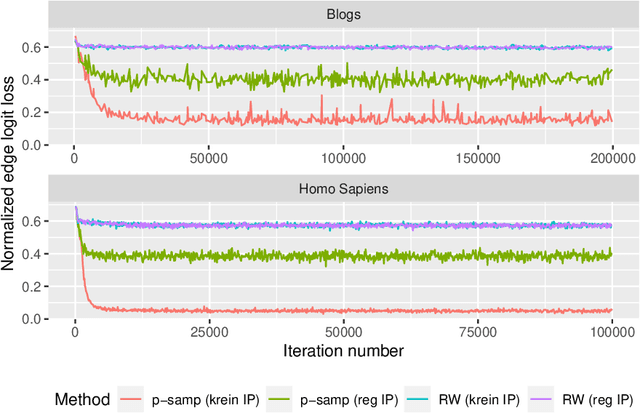
Jun 27, 2018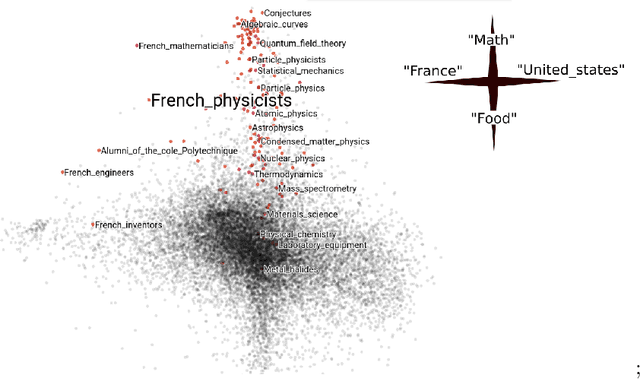


Abstract:Empirical risk minimization is the principal tool for prediction problems, but its extension to relational data remains unsolved. We solve this problem using recent advances in graph sampling theory. We (i) define an empirical risk for relational data and (ii) obtain stochastic gradients for this risk that are automatically unbiased. The key ingredient is to consider the method by which data is sampled from a graph as an explicit component of model design. Theoretical results establish that the choice of sampling scheme is critical. By integrating fast implementations of graph sampling schemes with standard automatic differentiation tools, we are able to solve the risk minimization in a plug-and-play fashion even on large datasets. We demonstrate empirically that relational ERM models achieve state-of-the-art results on semi-supervised node classification tasks. The experiments also confirm the importance of the choice of sampling scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge