A Unified MPC Strategy for a Tilt-rotor VTOL UAV Towards Seamless Mode Transitioning

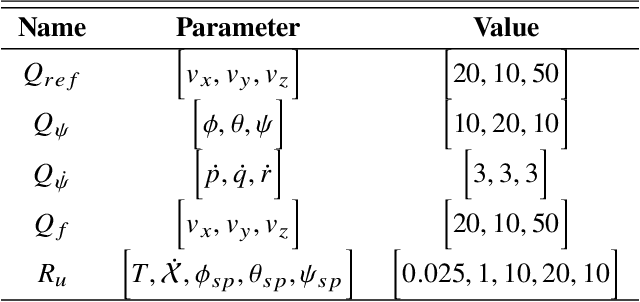
Capabilities of long-range flight and vertical take-off and landing (VTOL) are essential for Urban Air Mobility (UAM). Tiltrotor VTOLs have the advantage of balancing control simplicity and system complexity due to their redundant control authority. Prior work on controlling these aircraft either requires separate controllers and switching modes for different vehicle configurations or performs the control allocation on separate actuator sets, which cannot fully use the potential of the redundancy of tiltrotor. This paper introduces a unified MPC-based control strategy for a customized tiltrotor VTOL Unmanned Aerial Vehicle (UAV), which does not require mode-switching and can perform the control allocation in a consistent way. The incorporation of four independently controllable rotors in VTOL design offers an extra level of redundancy, allowing the VTOL to accommodate actuator failures. The result shows that our approach outperforms PID controllers while maintaining unified control. It allows the VTOL to perform smooth acceleration/deceleration, and precise coordinated turns. In addition, the independently controlled tilts enable the vehicle to handle actuator failures, ensuring that the aircraft remains operational even in the event of a servo or motor malfunction.

Inference on Optimal Dynamic Policies via Softmax Approximation

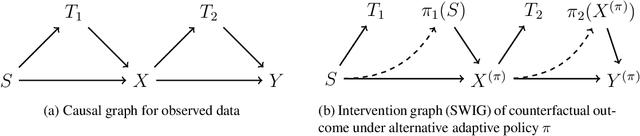
Estimating optimal dynamic policies from offline data is a fundamental problem in dynamic decision making. In the context of causal inference, the problem is known as estimating the optimal dynamic treatment regime. Even though there exists a plethora of methods for estimation, constructing confidence intervals for the value of the optimal regime and structural parameters associated with it is inherently harder, as it involves non-linear and non-differentiable functionals of un-known quantities that need to be estimated. Prior work resorted to sub-sample approaches that can deteriorate the quality of the estimate. We show that a simple soft-max approximation to the optimal treatment regime, for an appropriately fast growing temperature parameter, can achieve valid inference on the truly optimal regime. We illustrate our result for a two-period optimal dynamic regime, though our approach should directly extend to the finite horizon case. Our work combines techniques from semi-parametric inference and $g$-estimation, together with an appropriate triangular array central limit theorem, as well as a novel analysis of the asymptotic influence and asymptotic bias of softmax approximations.

Debiased Machine Learning without Sample-Splitting for Stable Estimators

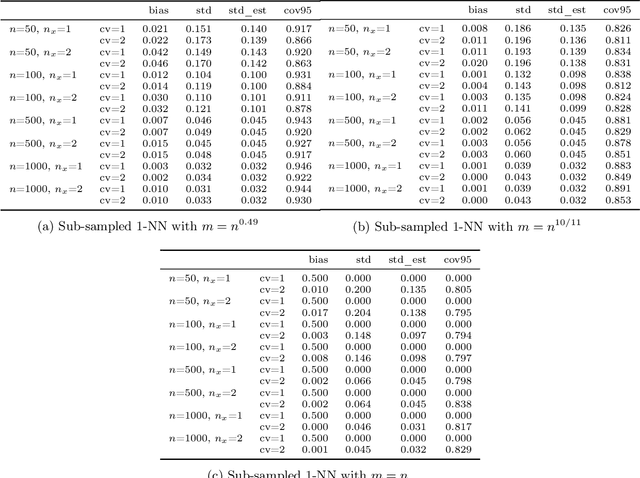
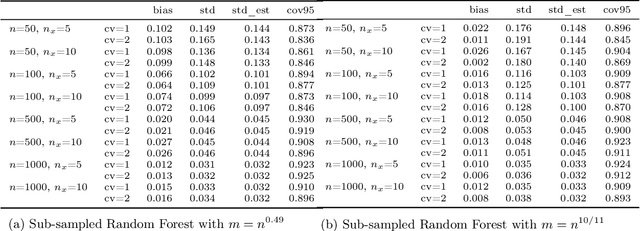
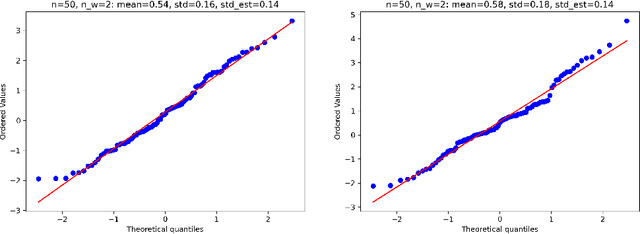
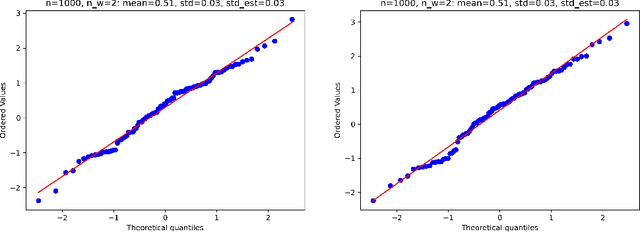
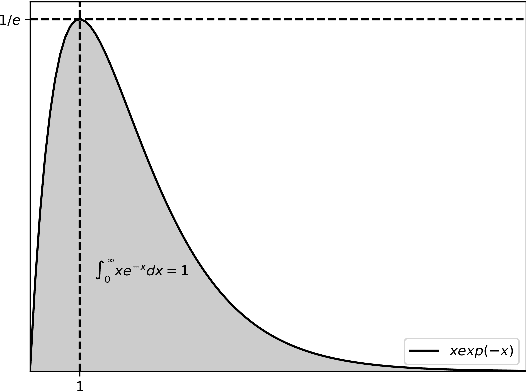
Estimation and inference on causal parameters is typically reduced to a generalized method of moments problem, which involves auxiliary functions that correspond to solutions to a regression or classification problem. Recent line of work on debiased machine learning shows how one can use generic machine learning estimators for these auxiliary problems, while maintaining asymptotic normality and root-$n$ consistency of the target parameter of interest, while only requiring mean-squared-error guarantees from the auxiliary estimation algorithms. The literature typically requires that these auxiliary problems are fitted on a separate sample or in a cross-fitting manner. We show that when these auxiliary estimation algorithms satisfy natural leave-one-out stability properties, then sample splitting is not required. This allows for sample re-use, which can be beneficial in moderately sized sample regimes. For instance, we show that the stability properties that we propose are satisfied for ensemble bagged estimators, built via sub-sampling without replacement, a popular technique in machine learning practice.