Fast and Scalable Spike and Slab Variable Selection in High-Dimensional Gaussian Processes

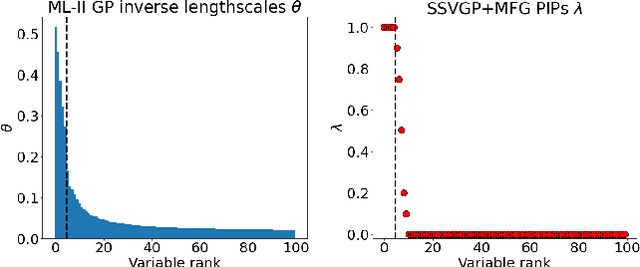
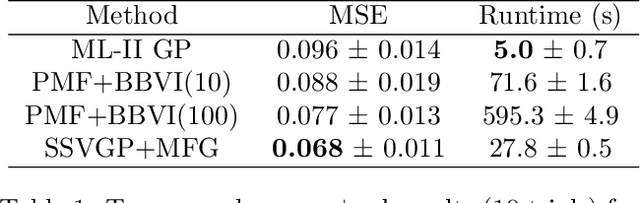
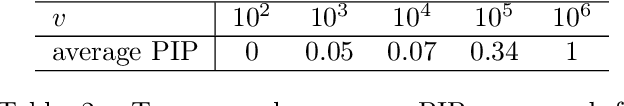
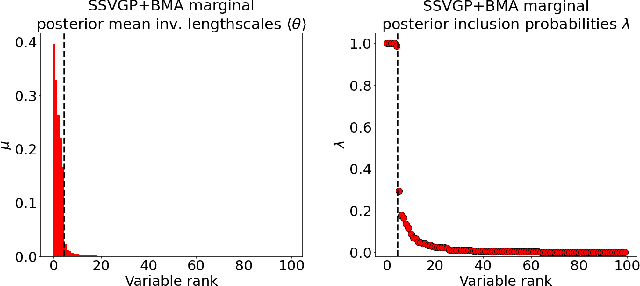
Variable selection in Gaussian processes (GPs) is typically undertaken by thresholding the inverse lengthscales of `automatic relevance determination' kernels, but in high-dimensional datasets this approach can be unreliable. A more probabilistically principled alternative is to use spike and slab priors and infer a posterior probability of variable inclusion. However, existing implementations in GPs are extremely costly to run in both high-dimensional and large-$n$ datasets, or are intractable for most kernels. As such, we develop a fast and scalable variational inference algorithm for the spike and slab GP that is tractable with arbitrary differentiable kernels. We improve our algorithm's ability to adapt to the sparsity of relevant variables by Bayesian model averaging over hyperparameters, and achieve substantial speed ups using zero temperature posterior restrictions, dropout pruning and nearest neighbour minibatching. In experiments our method consistently outperforms vanilla and sparse variational GPs whilst retaining similar runtimes (even when $n=10^6$) and performs competitively with a spike and slab GP using MCMC but runs up to $1000$ times faster.