Kenny Chiu
Randomization Tests for Conditional Group Symmetry
Dec 18, 2024Abstract:Symmetry plays a central role in the sciences, machine learning, and statistics. While statistical tests for the presence of distributional invariance with respect to groups have a long history, tests for conditional symmetry in the form of equivariance or conditional invariance are absent from the literature. This work initiates the study of nonparametric randomization tests for symmetry (invariance or equivariance) of a conditional distribution under the action of a specified locally compact group. We develop a general framework for randomization tests with finite-sample Type I error control and, using kernel methods, implement tests with finite-sample power lower bounds. We also describe and implement approximate versions of the tests, which are asymptotically consistent. We study their properties empirically on synthetic examples, and on applications to testing for symmetry in two problems from high-energy particle physics.
Non-parametric Hypothesis Tests for Distributional Group Symmetry
Jul 28, 2023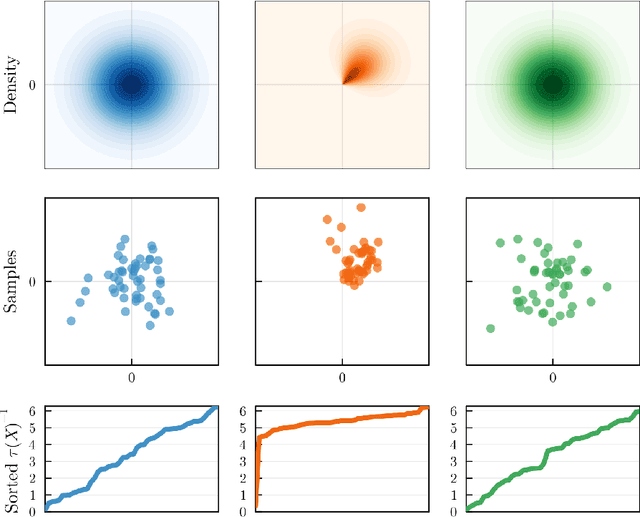
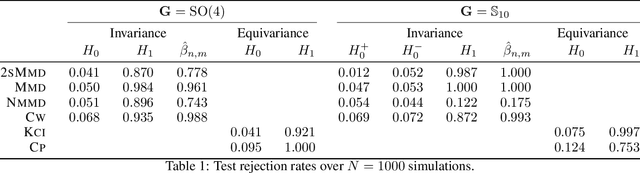
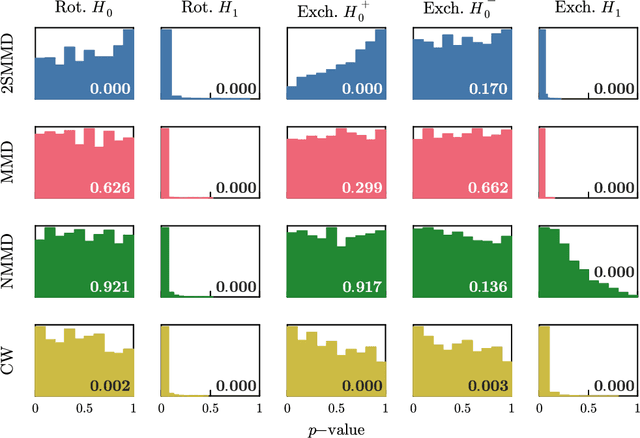

Abstract:Symmetry plays a central role in the sciences, machine learning, and statistics. For situations in which data are known to obey a symmetry, a multitude of methods that exploit symmetry have been developed. Statistical tests for the presence or absence of general group symmetry, however, are largely non-existent. This work formulates non-parametric hypothesis tests, based on a single independent and identically distributed sample, for distributional symmetry under a specified group. We provide a general formulation of tests for symmetry that apply to two broad settings. The first setting tests for the invariance of a marginal or joint distribution under the action of a compact group. Here, an asymptotically unbiased test only requires a computable metric on the space of probability distributions and the ability to sample uniformly random group elements. Building on this, we propose an easy-to-implement conditional Monte Carlo test and prove that it achieves exact $p$-values with finitely many observations and Monte Carlo samples. The second setting tests for the invariance or equivariance of a conditional distribution under the action of a locally compact group. We show that the test for conditional invariance or equivariance can be formulated as particular tests of conditional independence. We implement these tests from both settings using kernel methods and study them empirically on synthetic data. Finally, we apply them to testing for symmetry in geomagnetic satellite data and in two problems from high-energy particle physics.
Uncertainty in Neural Processes
Oct 08, 2020
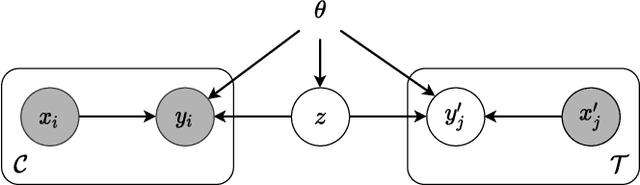
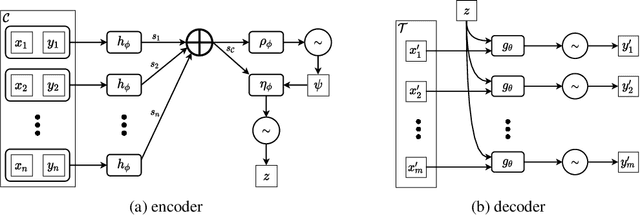
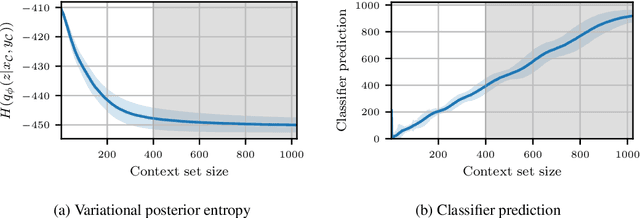
Abstract:We explore the effects of architecture and training objective choice on amortized posterior predictive inference in probabilistic conditional generative models. We aim this work to be a counterpoint to a recent trend in the literature that stresses achieving good samples when the amount of conditioning data is large. We instead focus our attention on the case where the amount of conditioning data is small. We highlight specific architecture and objective choices that we find lead to qualitative and quantitative improvement to posterior inference in this low data regime. Specifically we explore the effects of choices of pooling operator and variational family on posterior quality in neural processes. Superior posterior predictive samples drawn from our novel neural process architectures are demonstrated via image completion/in-painting experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge