Efficient Avoidance of Ellipsoidal Obstacles with Model Predictive Control for Mobile Robots and Vehicles

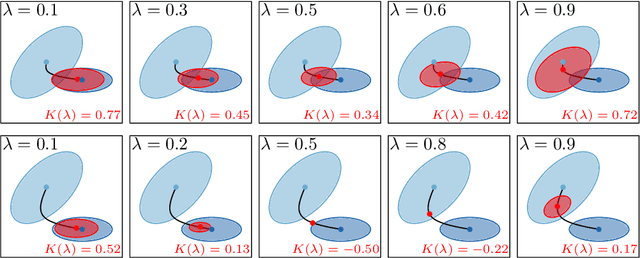
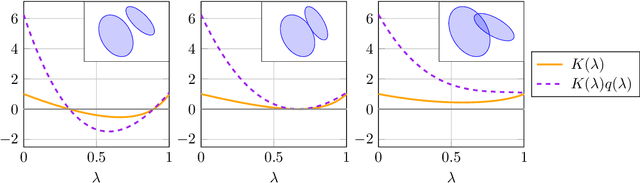
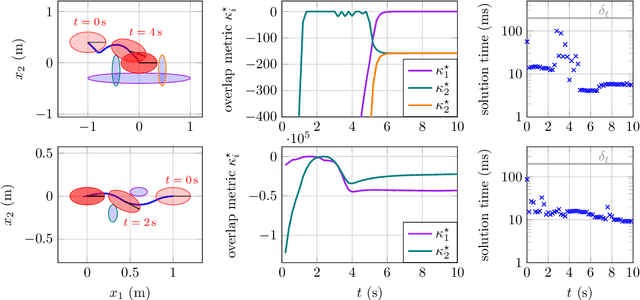
In real-world applications of mobile robots, collision avoidance is of critical importance. Typically, global motion planning in constrained environments is addressed through high-level control schemes. However, additionally integrating local collision avoidance into robot motion control offers significant advantages. For instance, it reduces the reliance on heuristics and conservatism that can arise from a two-stage approach separating local collision avoidance and control. Moreover, using model predictive control (MPC), a robot's full potential can be harnessed by considering jointly local collision avoidance, the robot's dynamics, and actuation constraints. In this context, the present paper focuses on obstacle avoidance for wheeled mobile robots, where both the robot's and obstacles' occupied volumes are modeled as ellipsoids. To this end, a computationally efficient overlap test, that works for arbitrary ellipsoids, is conducted and novelly integrated into the MPC framework. We propose a particularly efficient implementation tailored to robots moving in the plane. The functionality of the proposed obstacle-avoiding MPC is demonstrated for two exemplary types of kinematics by means of simulations. A hardware experiment using a real-world wheeled mobile robot shows transferability to reality and real-time applicability. The general computational approach to ellipsoidal obstacle avoidance can also be applied to other robotic systems and vehicles as well as three-dimensional scenarios.

Data-Driven Predictive Control of Nonholonomic Robots Based on a Bilinear Koopman Realization: Data Does Not Replace Geometry

Advances in machine learning and the growing trend towards effortless data generation in real-world systems has led to an increasing interest for data-inferred models and data-based control in robotics. It seems appealing to govern robots solely based on data, bypassing the traditional, more elaborate pipeline of system modeling through first-principles and subsequent controller design. One promising data-driven approach is the Extended Dynamic Mode Decomposition (EDMD) for control-affine systems, a system class which contains many vehicles and machines of immense practical importance including, e.g., typical wheeled mobile robots. EDMD can be highly data-efficient, computationally inexpensive, can deal with nonlinear dynamics as prevalent in robotics and mechanics, and has a sound theoretical foundation rooted in Koopman theory. On this background, this present paper examines how EDMD models can be integrated into predictive controllers for nonholonomic mobile robots. In addition to the conventional kinematic mobile robot, we also cover the complete data-driven control pipeline - from data acquisition to control design - when the robot is not treated in terms of first-order kinematics but in a second-order manner, allowing to account for actuator dynamics. Using only real-world measurement data, it is shown in both simulations and hardware experiments that the surrogate models enable high-precision predictive controllers in the studied cases. However, the findings raise significant concerns about purely data-centric approaches that overlook the underlying geometry of nonholonomic systems, showing that, for nonholonomic systems, some geometric insight seems necessary and cannot be easily compensated for with large amounts of data.

On Koopman-based surrogate models for non-holonomic robots

Data-driven surrogate models of dynamical systems based on the extended dynamic mode decomposition are nowadays well-established and widespread in applications. Further, for non-holonomic systems exhibiting a multiplicative coupling between states and controls, the usage of bi-linear surrogate models has proven beneficial. However, an in-depth analysis of the approximation quality and its dependence on different hyperparameters based on both simulation and experimental data is still missing. We investigate a differential-drive mobile robot to close this gap and provide first guidelines on the systematic design of data-efficient surrogate models.

Model Predictive Control of Non-Holonomic Vehicles: Beyond Differential-Drive

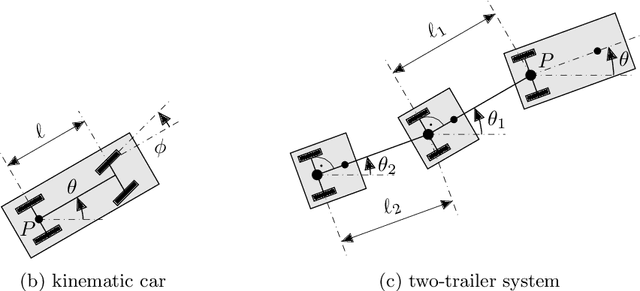
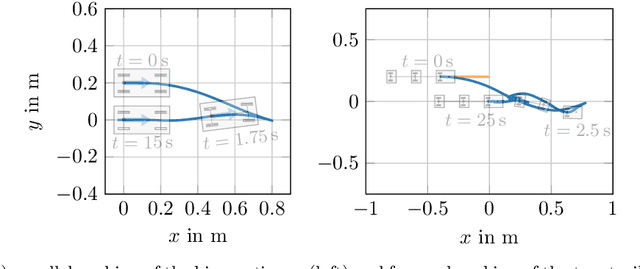
Non-holonomic vehicles are of immense practical value and increasingly subject to automation. However, controlling them accurately, e.g., when parking, is known to be challenging for automatic control methods, including model predictive control (MPC). Combining results from MPC theory and sub-Riemannian geometry in the form of homogeneous nilpotent system approximations, this paper proposes a comprehensive, ready-to-apply design procedure for MPC controllers to steer controllable, driftless non-holonomic vehicles into given setpoints. It can be ascertained that the resulting controllers nominally asymptotically stabilize the setpoint for a large-enough prediction horizon. The design procedure is exemplarily applied to four vehicles, including the kinematic car and a differentially driven mobile robot with up to two trailers. The controllers use a non-quadratic cost function tailored to the non-holonomic kinematics. Novelly, for the considered example vehicles, it is proven that a quadratic cost employed in an otherwise similar controller is insufficient to reliably asymptotically stabilize the closed loop. Since quadratic costs are the conventional choice in control, this highlights the relevance of the findings. To the knowledge of the authors, it is the first time that MPC controllers of the proposed structure are applied to non-holonomic vehicles beyond very simple ones, in particular (partly) on hardware.