Hendrik Carius
Efficient Avoidance of Ellipsoidal Obstacles with Model Predictive Control for Mobile Robots and Vehicles
Dec 16, 2024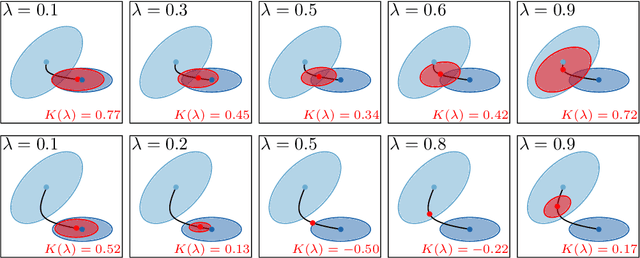
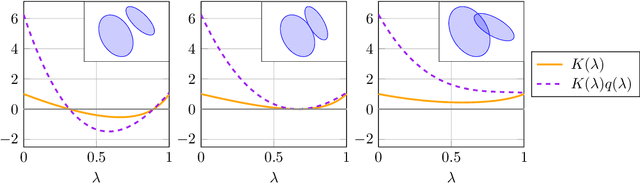
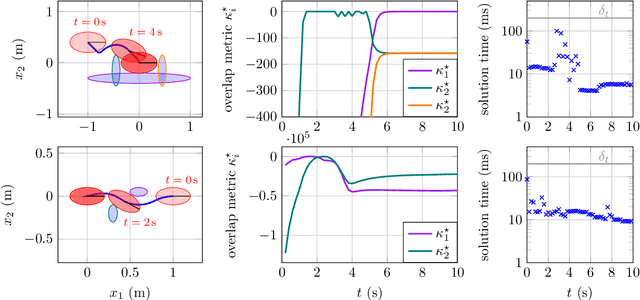

Abstract:In real-world applications of mobile robots, collision avoidance is of critical importance. Typically, global motion planning in constrained environments is addressed through high-level control schemes. However, additionally integrating local collision avoidance into robot motion control offers significant advantages. For instance, it reduces the reliance on heuristics and conservatism that can arise from a two-stage approach separating local collision avoidance and control. Moreover, using model predictive control (MPC), a robot's full potential can be harnessed by considering jointly local collision avoidance, the robot's dynamics, and actuation constraints. In this context, the present paper focuses on obstacle avoidance for wheeled mobile robots, where both the robot's and obstacles' occupied volumes are modeled as ellipsoids. To this end, a computationally efficient overlap test, that works for arbitrary ellipsoids, is conducted and novelly integrated into the MPC framework. We propose a particularly efficient implementation tailored to robots moving in the plane. The functionality of the proposed obstacle-avoiding MPC is demonstrated for two exemplary types of kinematics by means of simulations. A hardware experiment using a real-world wheeled mobile robot shows transferability to reality and real-time applicability. The general computational approach to ellipsoidal obstacle avoidance can also be applied to other robotic systems and vehicles as well as three-dimensional scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge