Robustness and Generalization in Quantum Reinforcement Learning via Lipschitz Regularization

Quantum machine learning leverages quantum computing to enhance accuracy and reduce model complexity compared to classical approaches, promising significant advancements in various fields. Within this domain, quantum reinforcement learning has garnered attention, often realized using variational quantum circuits to approximate the policy function. This paper addresses the robustness and generalization of quantum reinforcement learning by combining principles from quantum computing and control theory. Leveraging recent results on robust quantum machine learning, we utilize Lipschitz bounds to propose a regularized version of a quantum policy gradient approach, named the RegQPG algorithm. We show that training with RegQPG improves the robustness and generalization of the resulting policies. Furthermore, we introduce an algorithmic variant that incorporates curriculum learning, which minimizes failures during training. Our findings are validated through numerical experiments, demonstrating the practical benefits of our approach.

SafEDMD: A certified learning architecture tailored to data-driven control of nonlinear dynamical systems

The Koopman operator serves as the theoretical backbone for machine learning of dynamical control systems, where the operator is heuristically approximated by extended dynamic mode decomposition (EDMD). In this paper, we propose Stability- and certificate-oriented EDMD (SafEDMD): a novel EDMD-based learning architecture which comes along with rigorous certificates, resulting in a reliable surrogate model generated in a data-driven fashion. To ensure trustworthiness of SafEDMD, we derive proportional error bounds, which vanish at the origin and are tailored for control tasks, leading to certified controller design based on semi-definite programming. We illustrate the developed machinery by means of several benchmark examples and highlight the advantages over state-of-the-art methods.

Training robust and generalizable quantum models

Adversarial robustness and generalization are both crucial properties of reliable machine learning models. In this paper, we study these properties in the context of quantum machine learning based on Lipschitz bounds. We derive tailored, parameter-dependent Lipschitz bounds for quantum models with trainable encoding, showing that the norm of the data encoding has a crucial impact on the robustness against perturbations in the input data. Further, we derive a bound on the generalization error which explicitly depends on the parameters of the data encoding. Our theoretical findings give rise to a practical strategy for training robust and generalizable quantum models by regularizing the Lipschitz bound in the cost. Further, we show that, for fixed and non-trainable encodings as frequently employed in quantum machine learning, the Lipschitz bound cannot be influenced by tuning the parameters. Thus, trainable encodings are crucial for systematically adapting robustness and generalization during training. With numerical results, we demonstrate that, indeed, Lipschitz bound regularization leads to substantially more robust and generalizable quantum models.

Linear systems with neural network nonlinearities: Improved stability analysis via acausal Zames-Falb multipliers

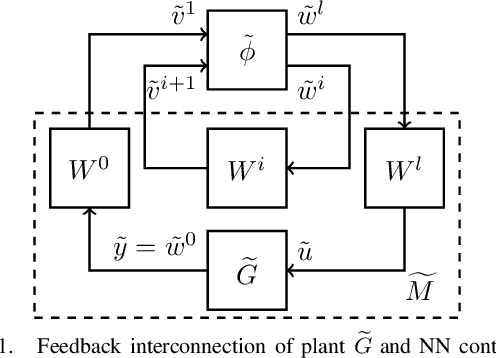
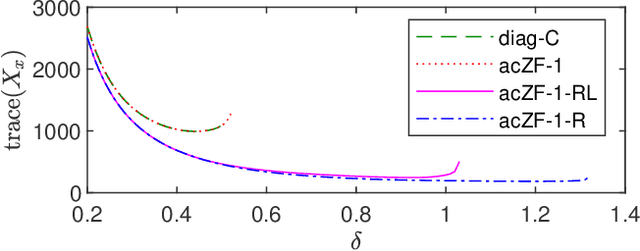
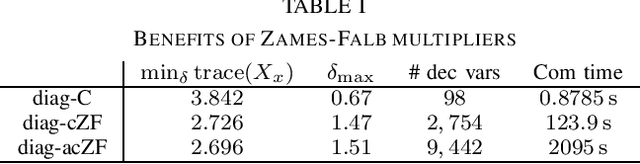
In this paper, we analyze the stability of feedback interconnections of a linear time-invariant system with a neural network nonlinearity in discrete time. Our analysis is based on abstracting neural networks using integral quadratic constraints (IQCs), exploiting the sector-bounded and slope-restricted structure of the underlying activation functions. In contrast to existing approaches, we leverage the full potential of dynamic IQCs to describe the nonlinear activation functions in a less conservative fashion. To be precise, we consider multipliers based on the full-block Yakubovich / circle criterion in combination with acausal Zames-Falb multipliers, leading to linear matrix inequality based stability certificates. Our approach provides a flexible and versatile framework for stability analysis of feedback interconnections with neural network nonlinearities, allowing to trade off computational efficiency and conservatism. Finally, we provide numerical examples that demonstrate the applicability of the proposed framework and the achievable improvements over previous approaches.

Offset-free setpoint tracking using neural network controllers

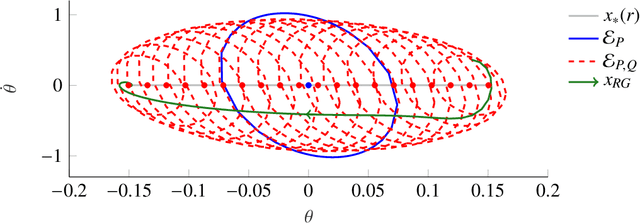
In this paper, we present a method to analyze local and global stability in offset-free setpoint tracking using neural network controllers and we provide ellipsoidal inner approximations of the corresponding region of attraction. We consider a feedback interconnection using a neural network controller in connection with an integrator, which allows for offset-free tracking of a desired piecewise constant reference that enters the controller as an external input. The feedback interconnection considered in this paper allows for general configurations of the neural network controller that include the special cases of output error and state feedback. Exploiting the fact that activation functions used in neural networks are slope-restricted, we derive linear matrix inequalities to verify stability using Lyapunov theory. After stating a global stability result, we present less conservative local stability conditions (i) for a given reference and (ii) for any reference from a certain set. The latter result even enables guaranteed tracking under setpoint changes using a reference governor which can lead to a significant increase of the region of attraction. Finally, we demonstrate the applicability of our analysis by verifying stability and offset-free tracking of a neural network controller that was trained to stabilize an inverted pendulum.

Training robust neural networks using Lipschitz bounds

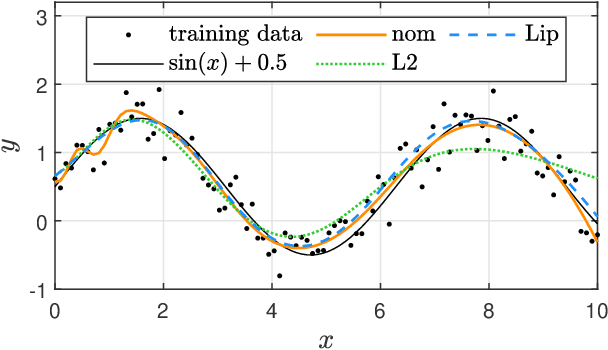
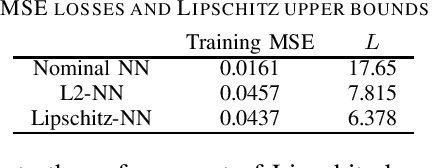
Due to their susceptibility to adversarial perturbations, neural networks (NNs) are hardly used in safety-critical applications. One measure of robustness to such perturbations in the input is the Lipschitz constant of the input-output map defined by an NN. In this work, we propose a framework to train NNs while at the same time encouraging robustness by keeping their Lipschitz constant small, thus addressing the robustness issue. More specifically, we design an optimization scheme based on the Alternating Direction Method of Multipliers that minimizes not only the training loss of an NN but also its Lipschitz constant resulting in a semidefinite programming based training procedure that promotes robustness. We design two versions of this training procedure. The first one includes a regularizer that penalizes an accurate upper bound on the Lipschitz constant. The second one allows to enforce a desired Lipschitz bound on the NN at all times during training. Finally, we provide two examples to show that the proposed framework successfully increases the robustness of NNs.