Linear systems with neural network nonlinearities: Improved stability analysis via acausal Zames-Falb multipliers
Paper and Code
Mar 31, 2021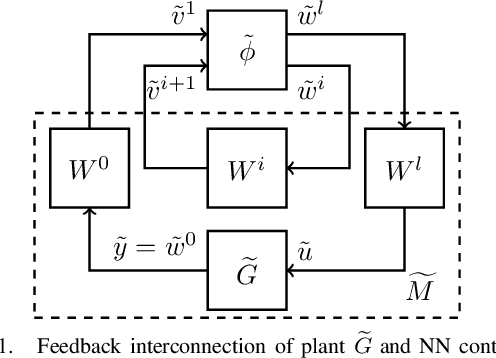
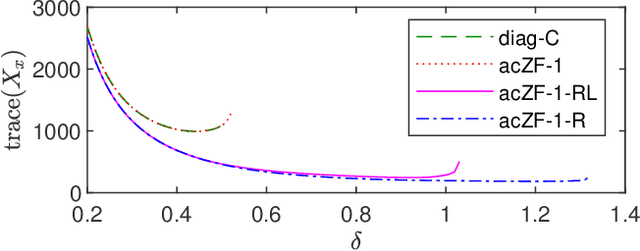
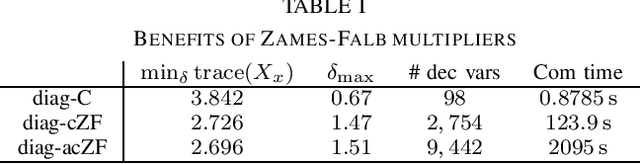
In this paper, we analyze the stability of feedback interconnections of a linear time-invariant system with a neural network nonlinearity in discrete time. Our analysis is based on abstracting neural networks using integral quadratic constraints (IQCs), exploiting the sector-bounded and slope-restricted structure of the underlying activation functions. In contrast to existing approaches, we leverage the full potential of dynamic IQCs to describe the nonlinear activation functions in a less conservative fashion. To be precise, we consider multipliers based on the full-block Yakubovich / circle criterion in combination with acausal Zames-Falb multipliers, leading to linear matrix inequality based stability certificates. Our approach provides a flexible and versatile framework for stability analysis of feedback interconnections with neural network nonlinearities, allowing to trade off computational efficiency and conservatism. Finally, we provide numerical examples that demonstrate the applicability of the proposed framework and the achievable improvements over previous approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge