CutReg: A loss regularizer for enhancing the scalability of QML via adaptive circuit cutting

Whether QML can offer a transformative advantage remains an open question. The severe constraints of NISQ hardware, particularly in circuit depth and connectivity, hinder both the validation of quantum advantage and the empirical investigation of major obstacles like barren plateaus. Circuit cutting techniques have emerged as a strategy to execute larger quantum circuits on smaller, less connected hardware by dividing them into subcircuits. However, this partitioning increases the number of samples needed to estimate the expectation value accurately through classical post-processing compared to estimating it directly from the full circuit. This work introduces a novel regularization term into the QML optimization process, directly penalizing the overhead associated with sampling. We demonstrate that this approach enables the optimizer to balance the advantages of gate cutting against the optimization of the typical ML cost function. Specifically, it navigates the trade-off between minimizing the cutting overhead and maintaining the overall accuracy of the QML model, paving the way to study larger complex problems in pursuit of quantum advantage.

Learning Encodings by Maximizing State Distinguishability: Variational Quantum Error Correction

Quantum error correction is crucial for protecting quantum information against decoherence. Traditional codes like the surface code require substantial overhead, making them impractical for near-term, early fault-tolerant devices. We propose a novel objective function for tailoring error correction codes to specific noise structures by maximizing the distinguishability between quantum states after a noise channel, ensuring efficient recovery operations. We formalize this concept with the distinguishability loss function, serving as a machine learning objective to discover resource-efficient encoding circuits optimized for given noise characteristics. We implement this methodology using variational techniques, termed variational quantum error correction (VarQEC). Our approach yields codes with desirable theoretical and practical properties and outperforms standard codes in various scenarios. We also provide proof-of-concept demonstrations on IBM and IQM hardware devices, highlighting the practical relevance of our procedure.

Optimizing Quantum Circuits via ZX Diagrams using Reinforcement Learning and Graph Neural Networks

Quantum computing is currently strongly limited by the impact of noise, in particular introduced by the application of two-qubit gates. For this reason, reducing the number of two-qubit gates is of paramount importance on noisy intermediate-scale quantum hardware. To advance towards more reliable quantum computing, we introduce a framework based on ZX calculus, graph-neural networks and reinforcement learning for quantum circuit optimization. By combining reinforcement learning and tree search, our method addresses the challenge of selecting optimal sequences of ZX calculus rewrite rules. Instead of relying on existing heuristic rules for minimizing circuits, our method trains a novel reinforcement learning policy that directly operates on ZX-graphs, therefore allowing us to search through the space of all possible circuit transformations to find a circuit significantly minimizing the number of CNOT gates. This way we can scale beyond hard-coded rules towards discovering arbitrary optimization rules. We demonstrate our method's competetiveness with state-of-the-art circuit optimizers and generalization capabilities on large sets of diverse random circuits.

Benchmarking Quantum Reinforcement Learning

Benchmarking and establishing proper statistical validation metrics for reinforcement learning (RL) remain ongoing challenges, where no consensus has been established yet. The emergence of quantum computing and its potential applications in quantum reinforcement learning (QRL) further complicate benchmarking efforts. To enable valid performance comparisons and to streamline current research in this area, we propose a novel benchmarking methodology, which is based on a statistical estimator for sample complexity and a definition of statistical outperformance. Furthermore, considering QRL, our methodology casts doubt on some previous claims regarding its superiority. We conducted experiments on a novel benchmarking environment with flexible levels of complexity. While we still identify possible advantages, our findings are more nuanced overall. We discuss the potential limitations of these results and explore their implications for empirical research on quantum advantage in QRL.

Fourier Analysis of Variational Quantum Circuits for Supervised Learning

VQC can be understood through the lens of Fourier analysis. It is already well-known that the function space represented by any circuit architecture can be described through a truncated Fourier sum. We show that the spectrum available to that truncated Fourier sum is not entirely determined by the encoding gates of the circuit, since the variational part of the circuit can constrain certain coefficients to zero, effectively removing that frequency from the spectrum. To the best of our knowledge, we give the first description of the functional dependence of the Fourier coefficients on the variational parameters as trigonometric polynomials. This allows us to provide an algorithm which computes the exact spectrum of any given circuit and the corresponding Fourier coefficients. Finally, we demonstrate that by comparing the Fourier transform of the dataset to the available spectra, it is possible to predict which VQC out of a given list of choices will be able to best fit the data.

Robustness and Generalization in Quantum Reinforcement Learning via Lipschitz Regularization

Quantum machine learning leverages quantum computing to enhance accuracy and reduce model complexity compared to classical approaches, promising significant advancements in various fields. Within this domain, quantum reinforcement learning has garnered attention, often realized using variational quantum circuits to approximate the policy function. This paper addresses the robustness and generalization of quantum reinforcement learning by combining principles from quantum computing and control theory. Leveraging recent results on robust quantum machine learning, we utilize Lipschitz bounds to propose a regularized version of a quantum policy gradient approach, named the RegQPG algorithm. We show that training with RegQPG improves the robustness and generalization of the resulting policies. Furthermore, we introduce an algorithmic variant that incorporates curriculum learning, which minimizes failures during training. Our findings are validated through numerical experiments, demonstrating the practical benefits of our approach.

Guided-SPSA: Simultaneous Perturbation Stochastic Approximation assisted by the Parameter Shift Rule

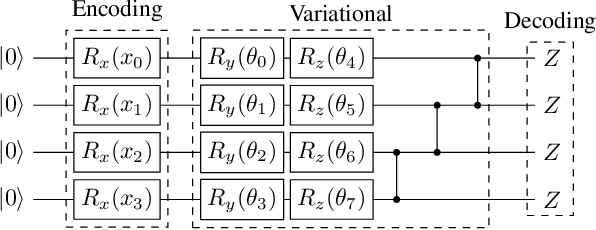
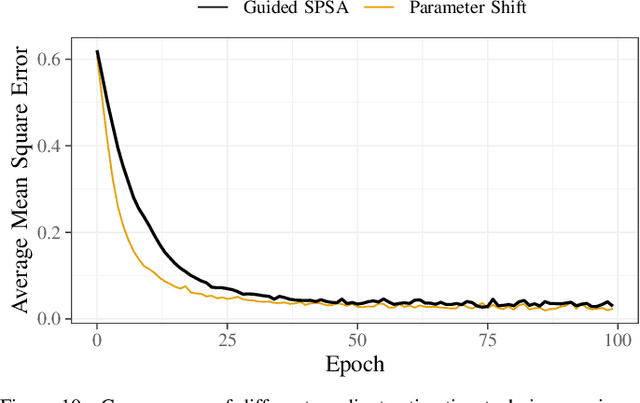
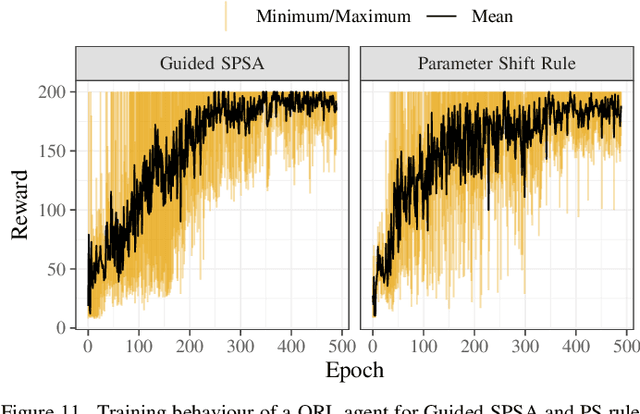
The study of variational quantum algorithms (VQCs) has received significant attention from the quantum computing community in recent years. These hybrid algorithms, utilizing both classical and quantum components, are well-suited for noisy intermediate-scale quantum devices. Though estimating exact gradients using the parameter-shift rule to optimize the VQCs is realizable in NISQ devices, they do not scale well for larger problem sizes. The computational complexity, in terms of the number of circuit evaluations required for gradient estimation by the parameter-shift rule, scales linearly with the number of parameters in VQCs. On the other hand, techniques that approximate the gradients of the VQCs, such as the simultaneous perturbation stochastic approximation (SPSA), do not scale with the number of parameters but struggle with instability and often attain suboptimal solutions. In this work, we introduce a novel gradient estimation approach called Guided-SPSA, which meaningfully combines the parameter-shift rule and SPSA-based gradient approximation. The Guided-SPSA results in a 15% to 25% reduction in the number of circuit evaluations required during training for a similar or better optimality of the solution found compared to the parameter-shift rule. The Guided-SPSA outperforms standard SPSA in all scenarios and outperforms the parameter-shift rule in scenarios such as suboptimal initialization of the parameters. We demonstrate numerically the performance of Guided-SPSA on different paradigms of quantum machine learning, such as regression, classification, and reinforcement learning.

Warm-Start Variational Quantum Policy Iteration

Reinforcement learning is a powerful framework aiming to determine optimal behavior in highly complex decision-making scenarios. This objective can be achieved using policy iteration, which requires to solve a typically large linear system of equations. We propose the variational quantum policy iteration (VarQPI) algorithm, realizing this step with a NISQ-compatible quantum-enhanced subroutine. Its scalability is supported by an analysis of the structure of generic reinforcement learning environments, laying the foundation for potential quantum advantage with utility-scale quantum computers. Furthermore, we introduce the warm-start initialization variant (WS-VarQPI) that significantly reduces resource overhead. The algorithm solves a large FrozenLake environment with an underlying 256x256-dimensional linear system, indicating its practical robustness.

Comprehensive Library of Variational LSE Solvers

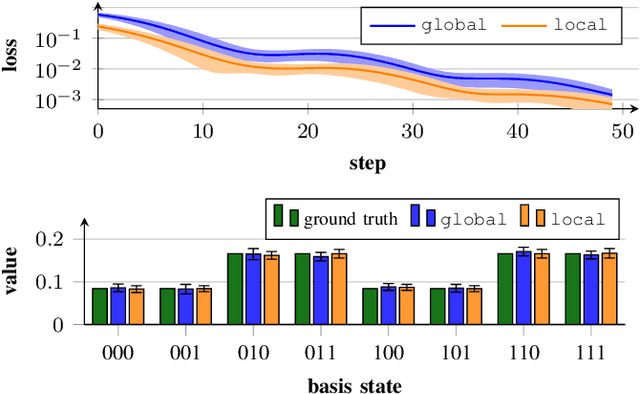
Linear systems of equations can be found in various mathematical domains, as well as in the field of machine learning. By employing noisy intermediate-scale quantum devices, variational solvers promise to accelerate finding solutions for large systems. Although there is a wealth of theoretical research on these algorithms, only fragmentary implementations exist. To fill this gap, we have developed the variational-lse-solver framework, which realizes existing approaches in literature, and introduces several enhancements. The user-friendly interface is designed for researchers that work at the abstraction level of identifying and developing end-to-end applications.

Qiskit-Torch-Module: Fast Prototyping of Quantum Neural Networks

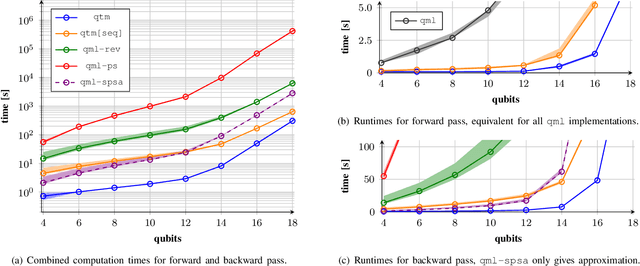
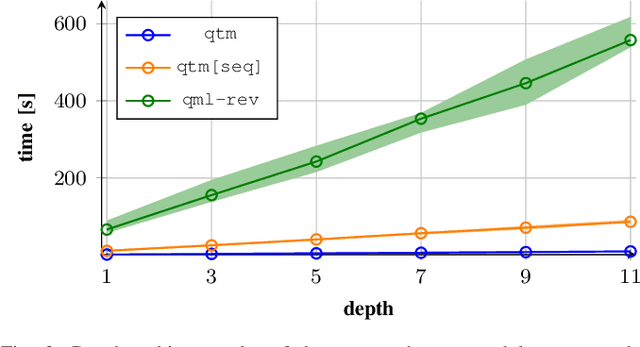
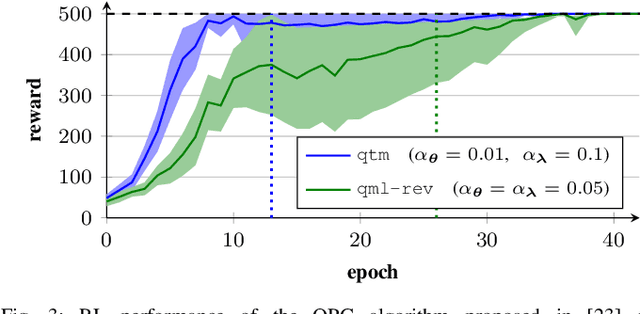
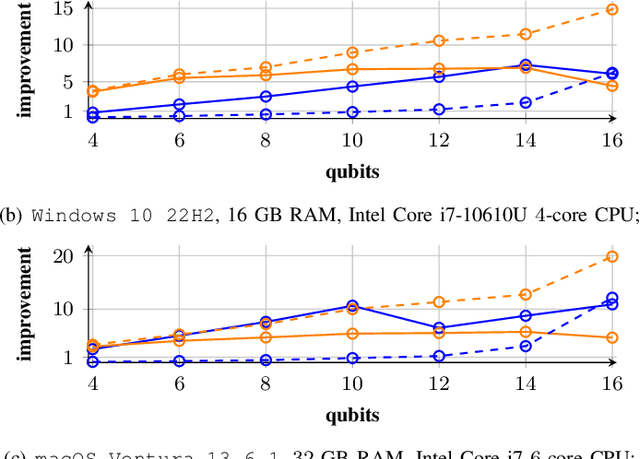
Quantum computer simulation software is an integral tool for the research efforts in the quantum computing community. An important aspect is the efficiency of respective frameworks, especially for training variational quantum algorithms. Focusing on the widely used Qiskit software environment, we develop the qiskit-torch-module. It improves runtime performance by two orders of magnitude over comparable libraries, while facilitating low-overhead integration with existing codebases. Moreover, the framework provides advanced tools for integrating quantum neural networks with PyTorch. The pipeline is tailored for single-machine compute systems, which constitute a widely employed setup in day-to-day research efforts.