Fourier Analysis of Variational Quantum Circuits for Supervised Learning

VQC can be understood through the lens of Fourier analysis. It is already well-known that the function space represented by any circuit architecture can be described through a truncated Fourier sum. We show that the spectrum available to that truncated Fourier sum is not entirely determined by the encoding gates of the circuit, since the variational part of the circuit can constrain certain coefficients to zero, effectively removing that frequency from the spectrum. To the best of our knowledge, we give the first description of the functional dependence of the Fourier coefficients on the variational parameters as trigonometric polynomials. This allows us to provide an algorithm which computes the exact spectrum of any given circuit and the corresponding Fourier coefficients. Finally, we demonstrate that by comparing the Fourier transform of the dataset to the available spectra, it is possible to predict which VQC out of a given list of choices will be able to best fit the data.

An Empirical Comparison of Optimizers for Quantum Machine Learning with SPSA-based Gradients

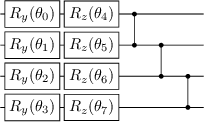
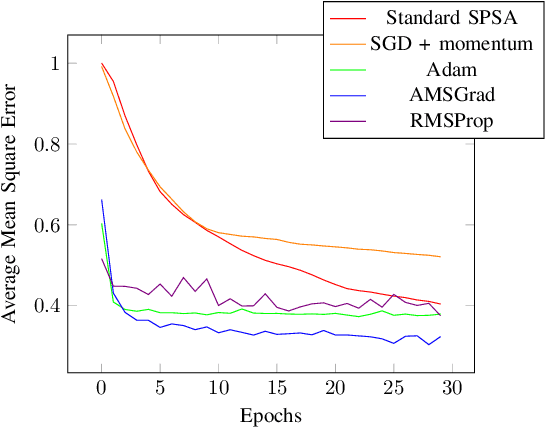
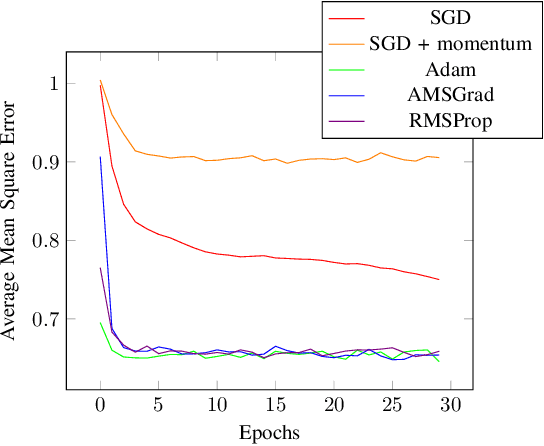
VQA have attracted a lot of attention from the quantum computing community for the last few years. Their hybrid quantum-classical nature with relatively shallow quantum circuits makes them a promising platform for demonstrating the capabilities of NISQ devices. Although the classical machine learning community focuses on gradient-based parameter optimization, finding near-exact gradients for VQC with the parameter-shift rule introduces a large sampling overhead. Therefore, gradient-free optimizers have gained popularity in quantum machine learning circles. Among the most promising candidates is the SPSA algorithm, due to its low computational cost and inherent noise resilience. We introduce a novel approach that uses the approximated gradient from SPSA in combination with state-of-the-art gradient-based classical optimizers. We demonstrate numerically that this outperforms both standard SPSA and the parameter-shift rule in terms of convergence rate and absolute error in simple regression tasks. The improvement of our novel approach over SPSA with stochastic gradient decent is even amplified when shot- and hardware-noise are taken into account. We also demonstrate that error mitigation does not significantly affect our results.

Batch Quantum Reinforcement Learning

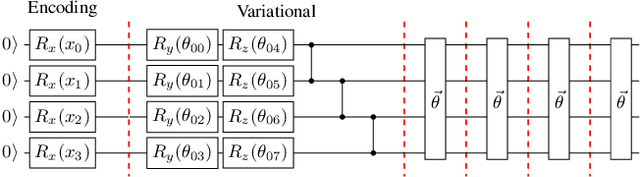
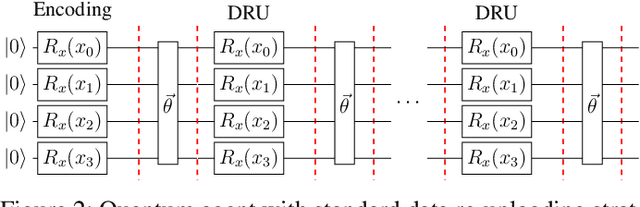
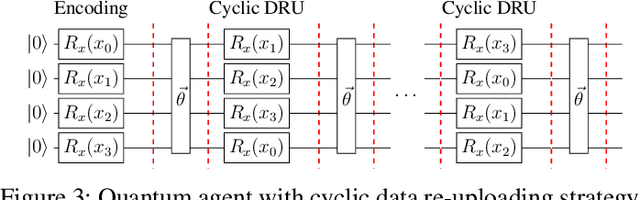
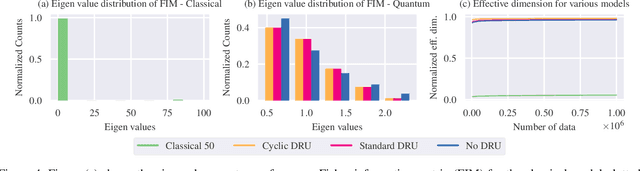
Training DRL agents is often a time-consuming process as a large number of samples and environment interactions is required. This effect is even amplified in the case of Batch RL, where the agent is trained without environment interactions solely based on a set of previously collected data. Novel approaches based on quantum computing suggest an advantage compared to classical approaches in terms of sample efficiency. To investigate this advantage, we propose a batch RL algorithm leveraging VQC as function approximators in the discrete BCQ algorithm. Additionally, we present a novel data re-uploading scheme based on cyclically shifting the input variables' order in the data encoding layers. We show the efficiency of our algorithm on the OpenAI CartPole environment and compare its performance to classical neural network-based discrete BCQ.