Benchmarking Quantum Reinforcement Learning

Benchmarking and establishing proper statistical validation metrics for reinforcement learning (RL) remain ongoing challenges, where no consensus has been established yet. The emergence of quantum computing and its potential applications in quantum reinforcement learning (QRL) further complicate benchmarking efforts. To enable valid performance comparisons and to streamline current research in this area, we propose a novel benchmarking methodology, which is based on a statistical estimator for sample complexity and a definition of statistical outperformance. Furthermore, considering QRL, our methodology casts doubt on some previous claims regarding its superiority. We conducted experiments on a novel benchmarking environment with flexible levels of complexity. While we still identify possible advantages, our findings are more nuanced overall. We discuss the potential limitations of these results and explore their implications for empirical research on quantum advantage in QRL.

Robustness and Generalization in Quantum Reinforcement Learning via Lipschitz Regularization

Quantum machine learning leverages quantum computing to enhance accuracy and reduce model complexity compared to classical approaches, promising significant advancements in various fields. Within this domain, quantum reinforcement learning has garnered attention, often realized using variational quantum circuits to approximate the policy function. This paper addresses the robustness and generalization of quantum reinforcement learning by combining principles from quantum computing and control theory. Leveraging recent results on robust quantum machine learning, we utilize Lipschitz bounds to propose a regularized version of a quantum policy gradient approach, named the RegQPG algorithm. We show that training with RegQPG improves the robustness and generalization of the resulting policies. Furthermore, we introduce an algorithmic variant that incorporates curriculum learning, which minimizes failures during training. Our findings are validated through numerical experiments, demonstrating the practical benefits of our approach.

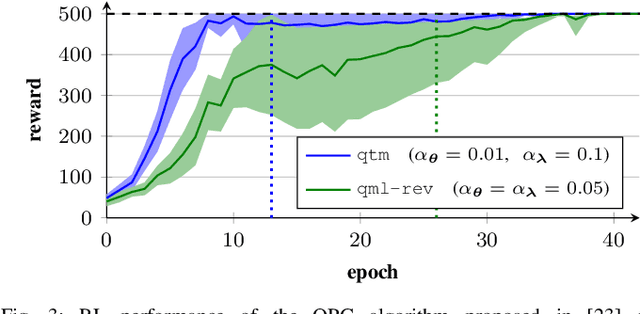
Warm-Start Variational Quantum Policy Iteration

Reinforcement learning is a powerful framework aiming to determine optimal behavior in highly complex decision-making scenarios. This objective can be achieved using policy iteration, which requires to solve a typically large linear system of equations. We propose the variational quantum policy iteration (VarQPI) algorithm, realizing this step with a NISQ-compatible quantum-enhanced subroutine. Its scalability is supported by an analysis of the structure of generic reinforcement learning environments, laying the foundation for potential quantum advantage with utility-scale quantum computers. Furthermore, we introduce the warm-start initialization variant (WS-VarQPI) that significantly reduces resource overhead. The algorithm solves a large FrozenLake environment with an underlying 256x256-dimensional linear system, indicating its practical robustness.

Comprehensive Library of Variational LSE Solvers

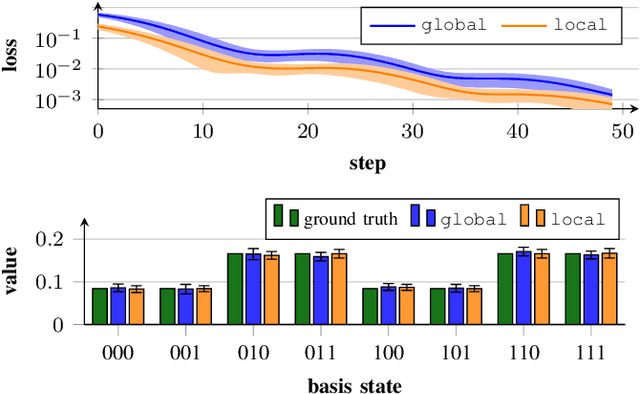
Linear systems of equations can be found in various mathematical domains, as well as in the field of machine learning. By employing noisy intermediate-scale quantum devices, variational solvers promise to accelerate finding solutions for large systems. Although there is a wealth of theoretical research on these algorithms, only fragmentary implementations exist. To fill this gap, we have developed the variational-lse-solver framework, which realizes existing approaches in literature, and introduces several enhancements. The user-friendly interface is designed for researchers that work at the abstraction level of identifying and developing end-to-end applications.

Qiskit-Torch-Module: Fast Prototyping of Quantum Neural Networks

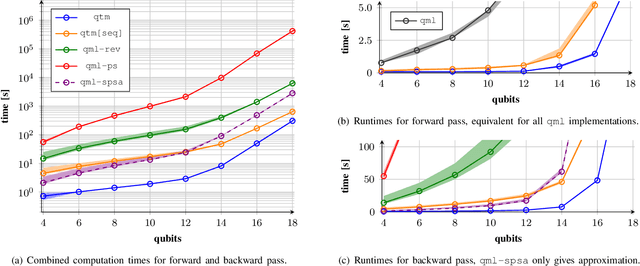
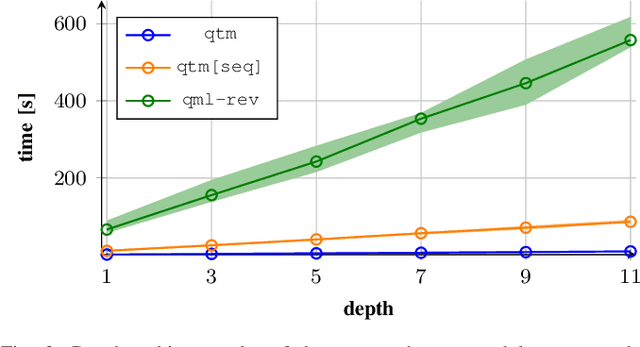
Quantum computer simulation software is an integral tool for the research efforts in the quantum computing community. An important aspect is the efficiency of respective frameworks, especially for training variational quantum algorithms. Focusing on the widely used Qiskit software environment, we develop the qiskit-torch-module. It improves runtime performance by two orders of magnitude over comparable libraries, while facilitating low-overhead integration with existing codebases. Moreover, the framework provides advanced tools for integrating quantum neural networks with PyTorch. The pipeline is tailored for single-machine compute systems, which constitute a widely employed setup in day-to-day research efforts.

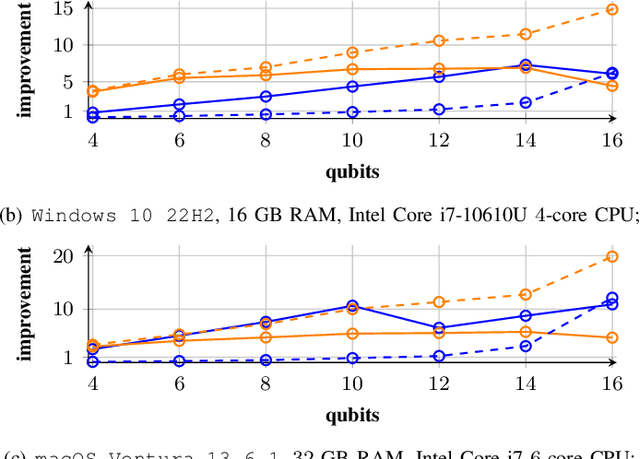
An Empirical Comparison of Optimizers for Quantum Machine Learning with SPSA-based Gradients

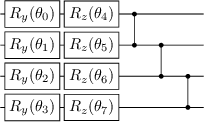
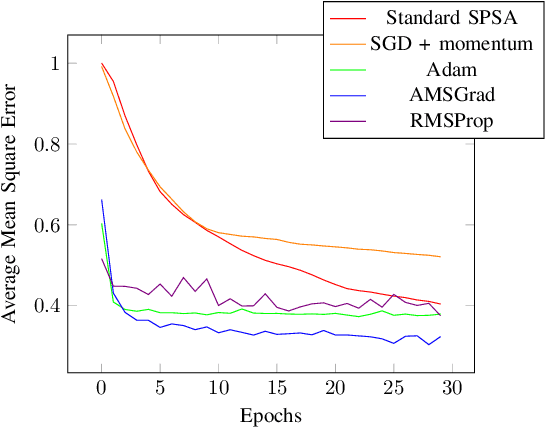
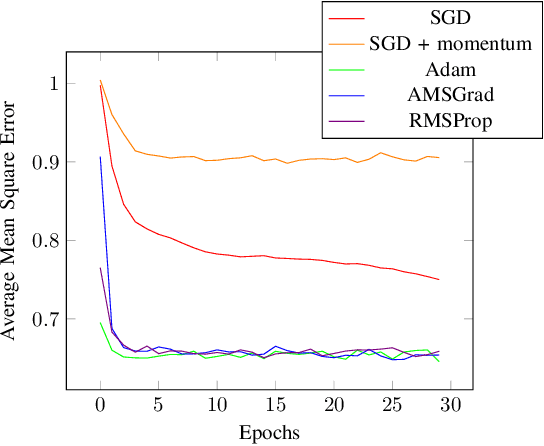
VQA have attracted a lot of attention from the quantum computing community for the last few years. Their hybrid quantum-classical nature with relatively shallow quantum circuits makes them a promising platform for demonstrating the capabilities of NISQ devices. Although the classical machine learning community focuses on gradient-based parameter optimization, finding near-exact gradients for VQC with the parameter-shift rule introduces a large sampling overhead. Therefore, gradient-free optimizers have gained popularity in quantum machine learning circles. Among the most promising candidates is the SPSA algorithm, due to its low computational cost and inherent noise resilience. We introduce a novel approach that uses the approximated gradient from SPSA in combination with state-of-the-art gradient-based classical optimizers. We demonstrate numerically that this outperforms both standard SPSA and the parameter-shift rule in terms of convergence rate and absolute error in simple regression tasks. The improvement of our novel approach over SPSA with stochastic gradient decent is even amplified when shot- and hardware-noise are taken into account. We also demonstrate that error mitigation does not significantly affect our results.

Incremental Data-Uploading for Full-Quantum Classification

The data representation in a machine-learning model strongly influences its performance. This becomes even more important for quantum machine learning models implemented on noisy intermediate scale quantum (NISQ) devices. Encoding high dimensional data into a quantum circuit for a NISQ device without any loss of information is not trivial and brings a lot of challenges. While simple encoding schemes (like single qubit rotational gates to encode high dimensional data) often lead to information loss within the circuit, complex encoding schemes with entanglement and data re-uploading lead to an increase in the encoding gate count. This is not well-suited for NISQ devices. This work proposes 'incremental data-uploading', a novel encoding pattern for high dimensional data that tackles these challenges. We spread the encoding gates for the feature vector of a given data point throughout the quantum circuit with parameterized gates in between them. This encoding pattern results in a better representation of data in the quantum circuit with a minimal pre-processing requirement. We show the efficiency of our encoding pattern on a classification task using the MNIST and Fashion-MNIST datasets, and compare different encoding methods via classification accuracy and the effective dimension of the model.