Jakob Murauer
Warm-Start Variational Quantum Policy Iteration
Apr 16, 2024Abstract:Reinforcement learning is a powerful framework aiming to determine optimal behavior in highly complex decision-making scenarios. This objective can be achieved using policy iteration, which requires to solve a typically large linear system of equations. We propose the variational quantum policy iteration (VarQPI) algorithm, realizing this step with a NISQ-compatible quantum-enhanced subroutine. Its scalability is supported by an analysis of the structure of generic reinforcement learning environments, laying the foundation for potential quantum advantage with utility-scale quantum computers. Furthermore, we introduce the warm-start initialization variant (WS-VarQPI) that significantly reduces resource overhead. The algorithm solves a large FrozenLake environment with an underlying 256x256-dimensional linear system, indicating its practical robustness.
Comprehensive Library of Variational LSE Solvers
Apr 15, 2024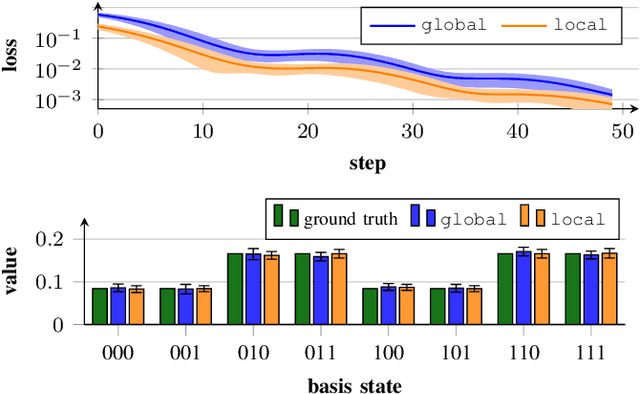


Abstract:Linear systems of equations can be found in various mathematical domains, as well as in the field of machine learning. By employing noisy intermediate-scale quantum devices, variational solvers promise to accelerate finding solutions for large systems. Although there is a wealth of theoretical research on these algorithms, only fragmentary implementations exist. To fill this gap, we have developed the variational-lse-solver framework, which realizes existing approaches in literature, and introduces several enhancements. The user-friendly interface is designed for researchers that work at the abstraction level of identifying and developing end-to-end applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge