Guided-SPSA: Simultaneous Perturbation Stochastic Approximation assisted by the Parameter Shift Rule
Paper and Code
Apr 24, 2024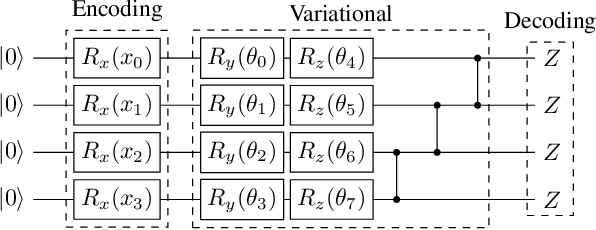
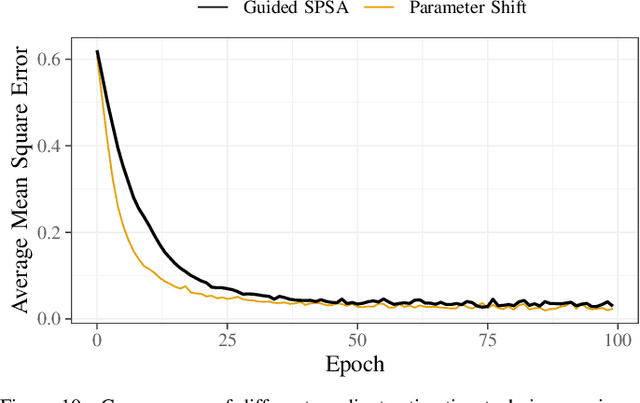
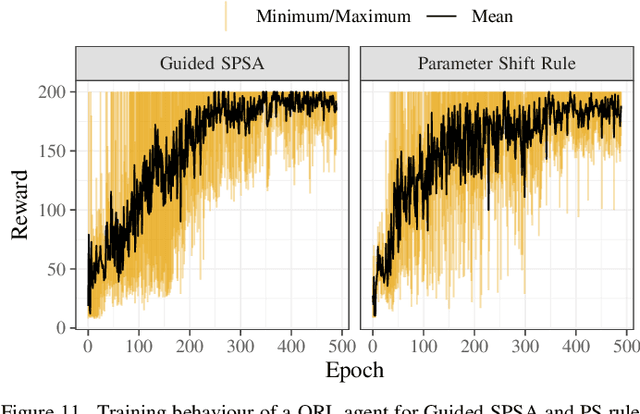

The study of variational quantum algorithms (VQCs) has received significant attention from the quantum computing community in recent years. These hybrid algorithms, utilizing both classical and quantum components, are well-suited for noisy intermediate-scale quantum devices. Though estimating exact gradients using the parameter-shift rule to optimize the VQCs is realizable in NISQ devices, they do not scale well for larger problem sizes. The computational complexity, in terms of the number of circuit evaluations required for gradient estimation by the parameter-shift rule, scales linearly with the number of parameters in VQCs. On the other hand, techniques that approximate the gradients of the VQCs, such as the simultaneous perturbation stochastic approximation (SPSA), do not scale with the number of parameters but struggle with instability and often attain suboptimal solutions. In this work, we introduce a novel gradient estimation approach called Guided-SPSA, which meaningfully combines the parameter-shift rule and SPSA-based gradient approximation. The Guided-SPSA results in a 15% to 25% reduction in the number of circuit evaluations required during training for a similar or better optimality of the solution found compared to the parameter-shift rule. The Guided-SPSA outperforms standard SPSA in all scenarios and outperforms the parameter-shift rule in scenarios such as suboptimal initialization of the parameters. We demonstrate numerically the performance of Guided-SPSA on different paradigms of quantum machine learning, such as regression, classification, and reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge