Data-Driven Reachability Analysis from Noisy Data

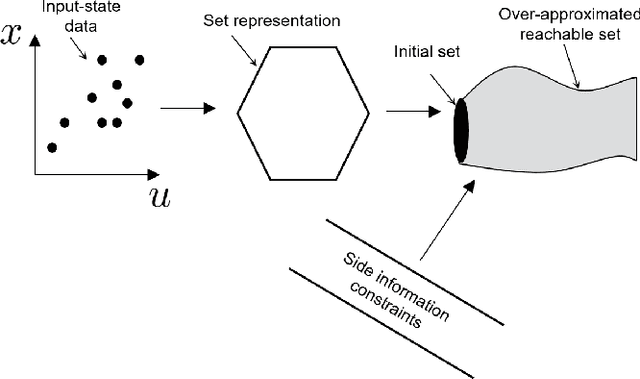
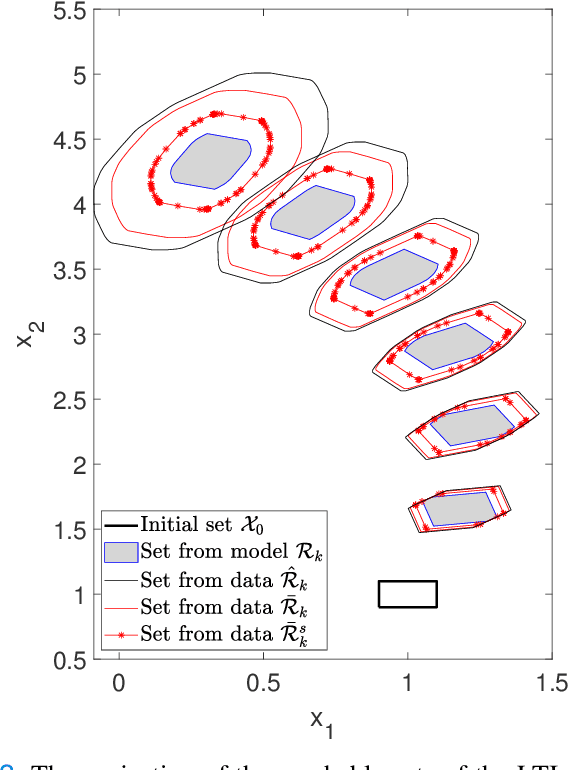
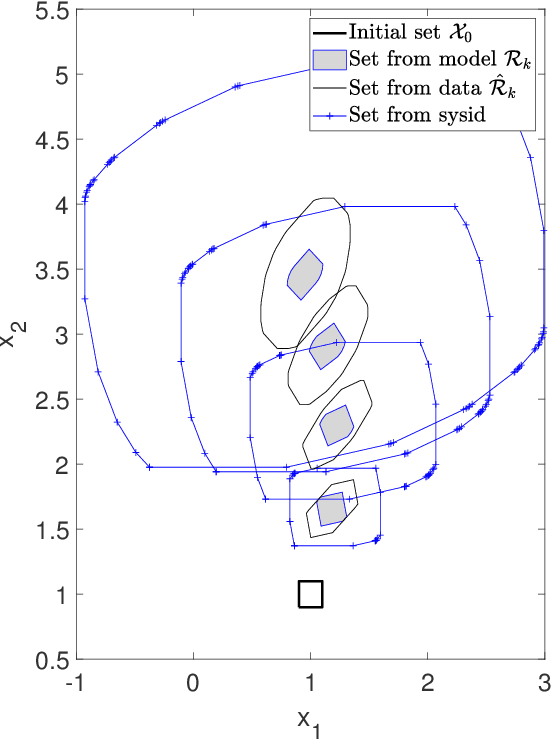
We consider the problem of computing reachable sets directly from noisy data without a given system model. Several reachability algorithms are presented, and their accuracy is shown to depend on the underlying system generating the data. First, an algorithm for computing over-approximated reachable sets based on matrix zonotopes is proposed for linear systems. Constrained matrix zonotopes are introduced to provide less conservative reachable sets at the cost of increased computational expenses and utilized to incorporate prior knowledge about the unknown system model. Then we extend the approach to polynomial systems and under the assumption of Lipschitz continuity to nonlinear systems. Theoretical guarantees are given for these algorithms in that they give a proper over-approximative reachable set containing the true reachable set. Multiple numerical examples show the applicability of the introduced algorithms, and accuracy comparisons are made between algorithms.

Offset-free setpoint tracking using neural network controllers

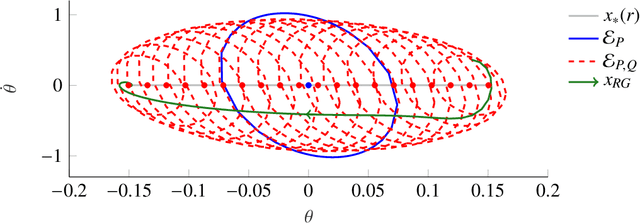
In this paper, we present a method to analyze local and global stability in offset-free setpoint tracking using neural network controllers and we provide ellipsoidal inner approximations of the corresponding region of attraction. We consider a feedback interconnection using a neural network controller in connection with an integrator, which allows for offset-free tracking of a desired piecewise constant reference that enters the controller as an external input. The feedback interconnection considered in this paper allows for general configurations of the neural network controller that include the special cases of output error and state feedback. Exploiting the fact that activation functions used in neural networks are slope-restricted, we derive linear matrix inequalities to verify stability using Lyapunov theory. After stating a global stability result, we present less conservative local stability conditions (i) for a given reference and (ii) for any reference from a certain set. The latter result even enables guaranteed tracking under setpoint changes using a reference governor which can lead to a significant increase of the region of attraction. Finally, we demonstrate the applicability of our analysis by verifying stability and offset-free tracking of a neural network controller that was trained to stabilize an inverted pendulum.

Data-Driven Reachability Analysis Using Matrix Zonotopes

In this paper, we propose a data-driven reachability analysis approach for an unknown control system. Reachability analysis is an essential tool for guaranteeing safety properties. However, most current reachability analysis heavily relies on the existence of a suitable system model, which is often not directly available in practice. We instead propose a reachability analysis approach based on noisy data. More specifically, we first provide an algorithm for over-approximating the reachable set of a linear time-invariant system using matrix zonotopes. Then we introduce an extension for nonlinear systems. We provide theoretical guarantees in both cases. Numerical examples show the potential and applicability of the introduced methods.

Training robust neural networks using Lipschitz bounds

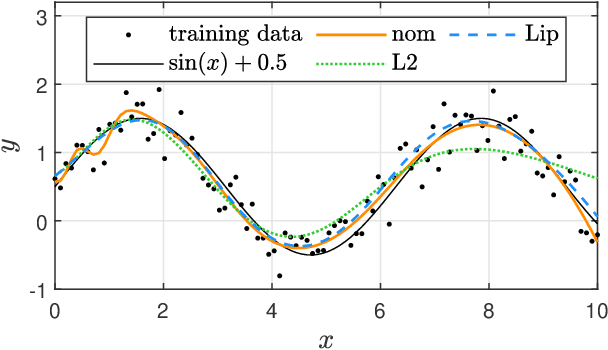
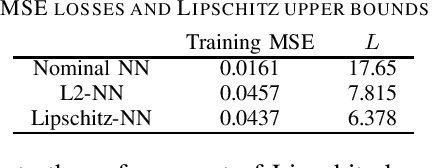
Due to their susceptibility to adversarial perturbations, neural networks (NNs) are hardly used in safety-critical applications. One measure of robustness to such perturbations in the input is the Lipschitz constant of the input-output map defined by an NN. In this work, we propose a framework to train NNs while at the same time encouraging robustness by keeping their Lipschitz constant small, thus addressing the robustness issue. More specifically, we design an optimization scheme based on the Alternating Direction Method of Multipliers that minimizes not only the training loss of an NN but also its Lipschitz constant resulting in a semidefinite programming based training procedure that promotes robustness. We design two versions of this training procedure. The first one includes a regularizer that penalizes an accurate upper bound on the Lipschitz constant. The second one allows to enforce a desired Lipschitz bound on the NN at all times during training. Finally, we provide two examples to show that the proposed framework successfully increases the robustness of NNs.