Data-Driven Reachability Analysis from Noisy Data
Paper and Code
May 15, 2021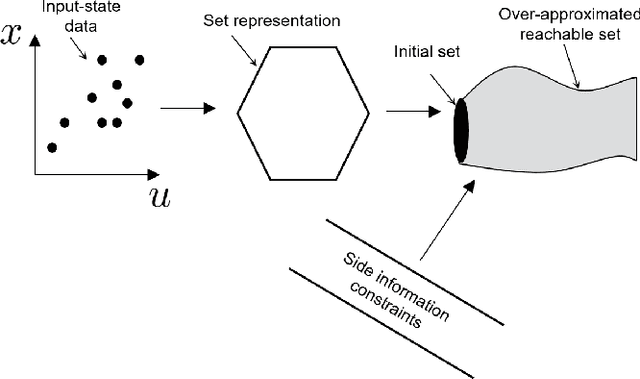
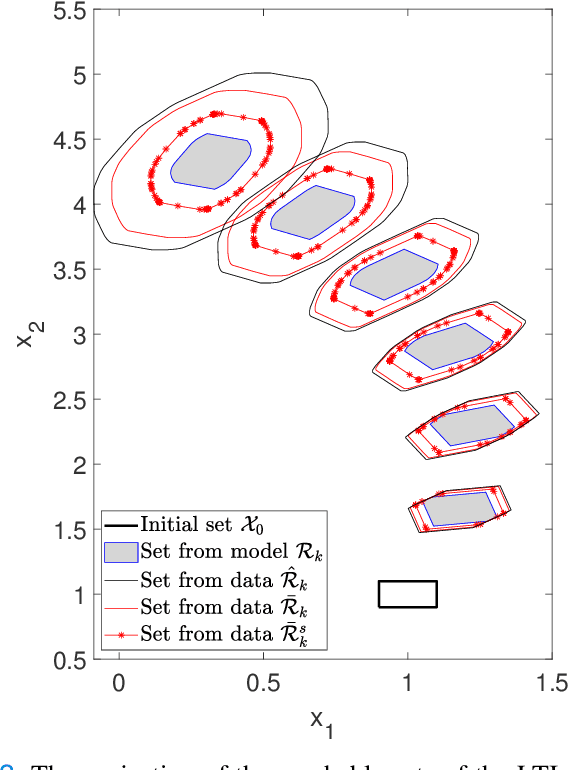
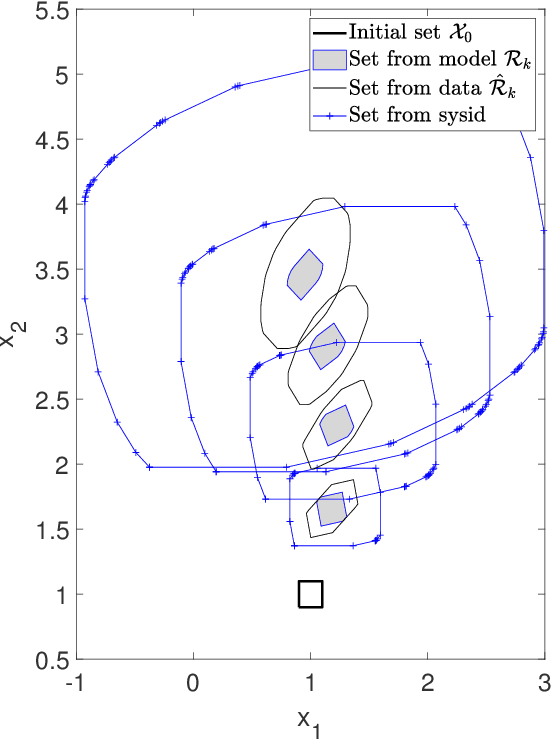

We consider the problem of computing reachable sets directly from noisy data without a given system model. Several reachability algorithms are presented, and their accuracy is shown to depend on the underlying system generating the data. First, an algorithm for computing over-approximated reachable sets based on matrix zonotopes is proposed for linear systems. Constrained matrix zonotopes are introduced to provide less conservative reachable sets at the cost of increased computational expenses and utilized to incorporate prior knowledge about the unknown system model. Then we extend the approach to polynomial systems and under the assumption of Lipschitz continuity to nonlinear systems. Theoretical guarantees are given for these algorithms in that they give a proper over-approximative reachable set containing the true reachable set. Multiple numerical examples show the applicability of the introduced algorithms, and accuracy comparisons are made between algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge