Variational Selection of Features for Molecular Kinetics

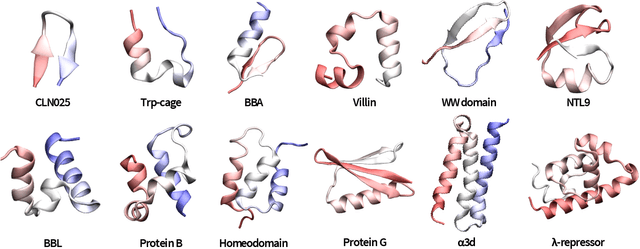
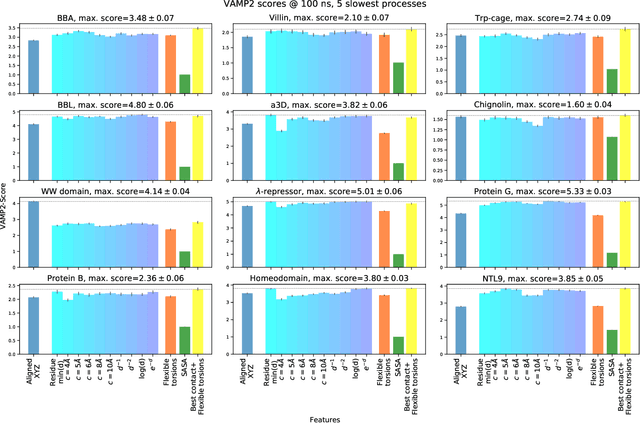
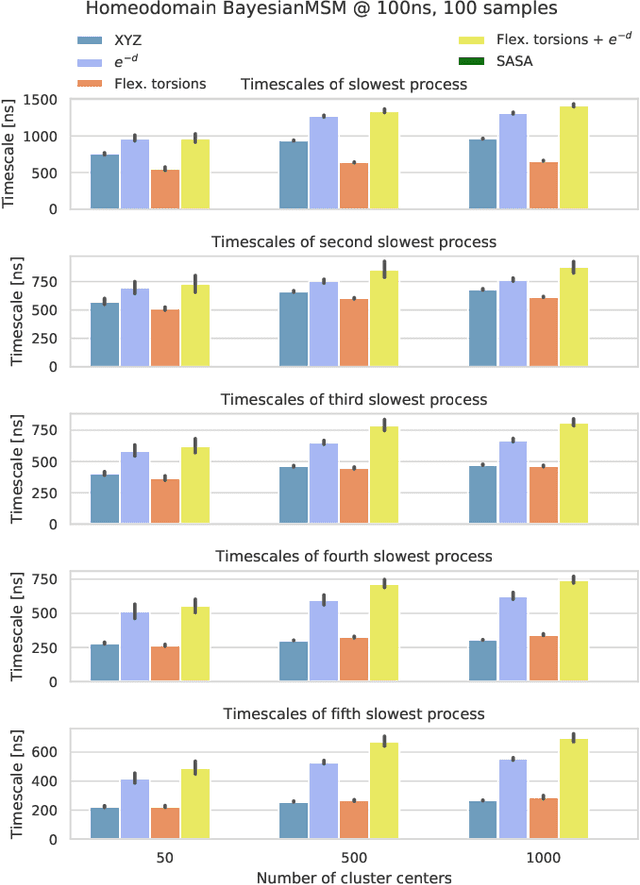
The modeling of atomistic biomolecular simulations using kinetic models such as Markov state models (MSMs) has had many notable algorithmic advances in recent years. The variational principle has opened the door for a nearly fully automated toolkit for selecting models that predict the long-time kinetics from molecular dynamics simulations. However, one yet-unoptimized step of the pipeline involves choosing the features, or collective variables, from which the model should be constructed. In order to build intuitive models, these collective variables are often sought to be interpretable and familiar features, such as torsional angles or contact distances in a protein structure. However, previous approaches for evaluating the chosen features rely on constructing a full MSM, which in turn requires additional hyperparameters to be chosen, and hence leads to a computationally expensive framework. Here, we present a method to optimize the feature choice directly, without requiring the construction of the final kinetic model. We demonstrate our rigorous preprocessing algorithm on a canonical set of twelve fast-folding protein simulations, and show that our procedure leads to more efficient model selection.

Variational Koopman models: slow collective variables and molecular kinetics from short off-equilibrium simulations

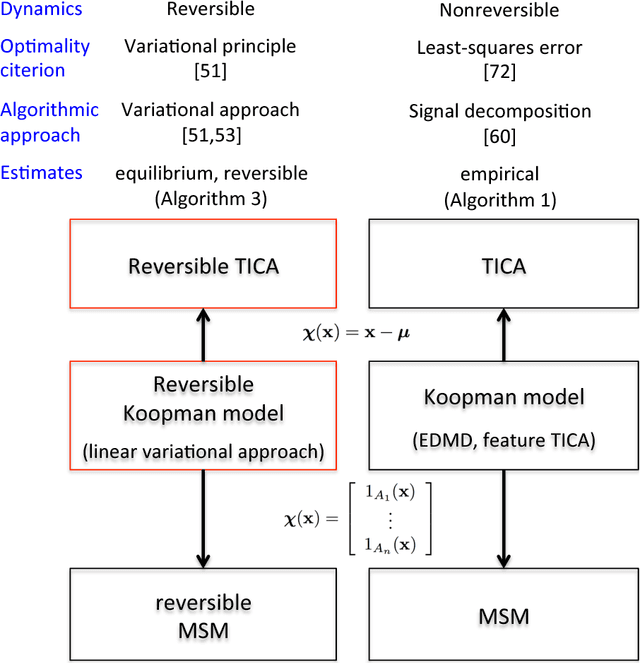
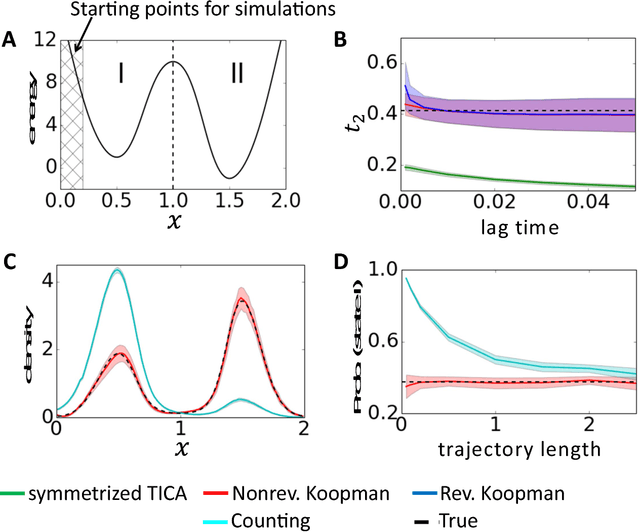
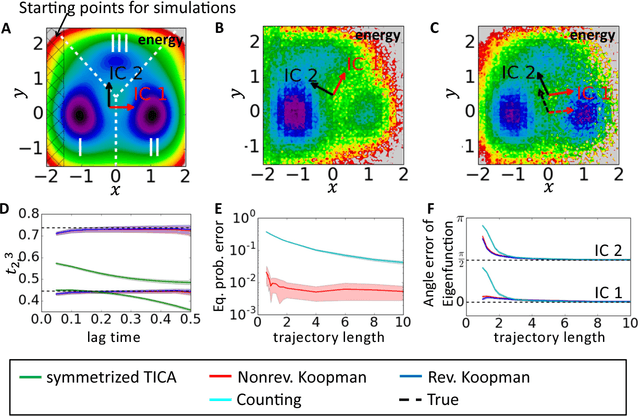
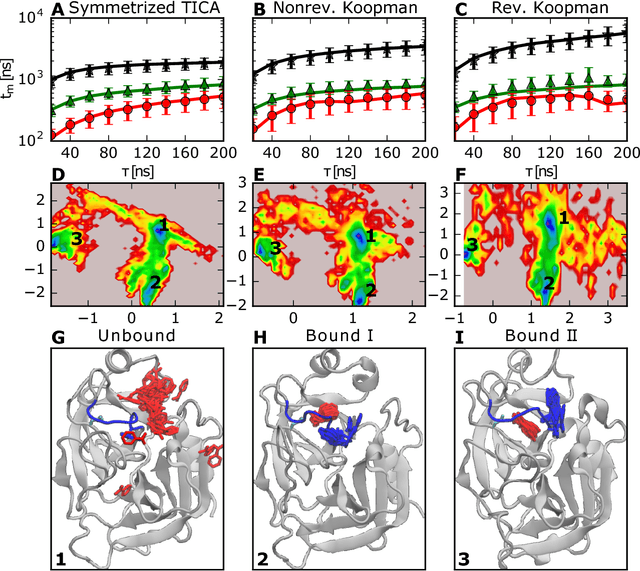
Markov state models (MSMs) and Master equation models are popular approaches to approximate molecular kinetics, equilibria, metastable states, and reaction coordinates in terms of a state space discretization usually obtained by clustering. Recently, a powerful generalization of MSMs has been introduced, the variational approach (VA) of molecular kinetics and its special case the time-lagged independent component analysis (TICA), which allow us to approximate slow collective variables and molecular kinetics by linear combinations of smooth basis functions or order parameters. While it is known how to estimate MSMs from trajectories whose starting points are not sampled from an equilibrium ensemble, this has not yet been the case for TICA and the VA. Previous estimates from short trajectories, have been strongly biased and thus not variationally optimal. Here, we employ Koopman operator theory and ideas from dynamic mode decomposition (DMD) to extend the VA and TICA to non-equilibrium data. The main insight is that the VA and TICA provide a coefficient matrix that we call Koopman model, as it approximates the underlying dynamical (Koopman) operator in conjunction with the basis set used. This Koopman model can be used to compute a stationary vector to reweight the data to equilibrium. From such a Koopman-reweighted sample, equilibrium expectation values and variationally optimal reversible Koopman models can be constructed even with short simulations. The Koopman model can be used to propagate densities, and its eigenvalue decomposition provide estimates of relaxation timescales and slow collective variables for dimension reduction. Koopman models are generalizations of Markov state models, TICA and the linear VA and allow molecular kinetics to be described without a cluster discretization.