Neural parameter calibration and uncertainty quantification for epidemic forecasting

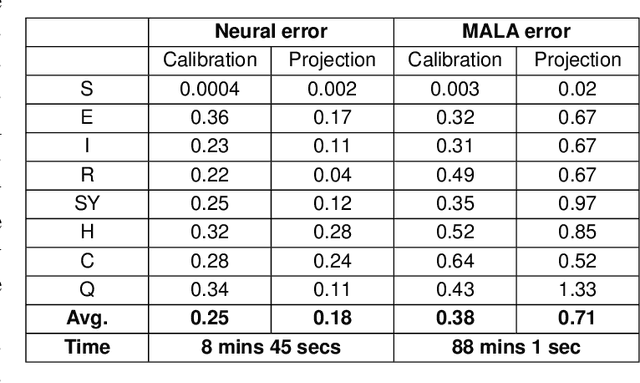
The recent COVID-19 pandemic has thrown the importance of accurately forecasting contagion dynamics and learning infection parameters into sharp focus. At the same time, effective policy-making requires knowledge of the uncertainty on such predictions, in order, for instance, to be able to ready hospitals and intensive care units for a worst-case scenario without needlessly wasting resources. In this work, we apply a novel and powerful computational method to the problem of learning probability densities on contagion parameters and providing uncertainty quantification for pandemic projections. Using a neural network, we calibrate an ODE model to data of the spread of COVID-19 in Berlin in 2020, achieving both a significantly more accurate calibration and prediction than Markov-Chain Monte Carlo (MCMC)-based sampling schemes. The uncertainties on our predictions provide meaningful confidence intervals e.g. on infection figures and hospitalisation rates, while training and running the neural scheme takes minutes where MCMC takes hours. We show convergence of our method to the true posterior on a simplified SIR model of epidemics, and also demonstrate our method's learning capabilities on a reduced dataset, where a complex model is learned from a small number of compartments for which data is available.

GraphKKE: Graph Kernel Koopman Embedding for Human Microbiome Analysis

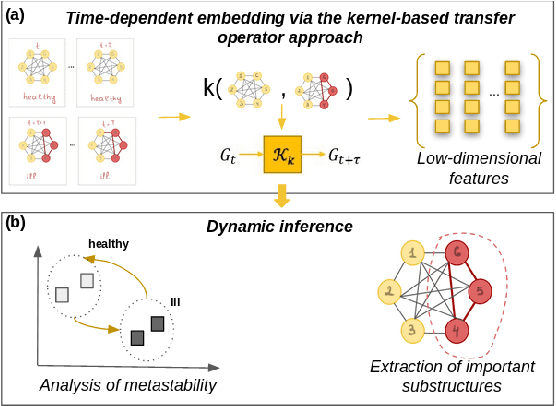
More and more diseases have been found to be strongly correlated with disturbances in the microbiome constitution, e.g., obesity, diabetes, or some cancer types. Thanks to modern high-throughput omics technologies, it becomes possible to directly analyze human microbiome and its influence on the health status. Microbial communities are monitored over long periods of time and the associations between their members are explored. These relationships can be described by a time-evolving graph. In order to understand responses of the microbial community members to a distinct range of perturbations such as antibiotics exposure or diseases and general dynamical properties, the time-evolving graph of the human microbial communities has to be analyzed. This becomes especially challenging due to dozens of complex interactions among microbes and metastable dynamics. The key to solving this problem is the representation of the time-evolving graphs as fixed-length feature vectors preserving the original dynamics. We propose a method for learning the embedding of the time-evolving graph that is based on the spectral analysis of transfer operators and graph kernels. We demonstrate that our method can capture temporary changes in the time-evolving graph on both created synthetic data and real-world data. Our experiments demonstrate the efficacy of the method. Furthermore, we show that our method can be applied to human microbiome data to study dynamic processes.

Sparse Proteomics Analysis - A compressed sensing-based approach for feature selection and classification of high-dimensional proteomics mass spectrometry data

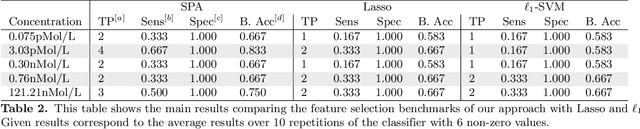
Background: High-throughput proteomics techniques, such as mass spectrometry (MS)-based approaches, produce very high-dimensional data-sets. In a clinical setting one is often interested in how mass spectra differ between patients of different classes, for example spectra from healthy patients vs. spectra from patients having a particular disease. Machine learning algorithms are needed to (a) identify these discriminating features and (b) classify unknown spectra based on this feature set. Since the acquired data is usually noisy, the algorithms should be robust against noise and outliers, while the identified feature set should be as small as possible. Results: We present a new algorithm, Sparse Proteomics Analysis (SPA), based on the theory of compressed sensing that allows us to identify a minimal discriminating set of features from mass spectrometry data-sets. We show (1) how our method performs on artificial and real-world data-sets, (2) that its performance is competitive with standard (and widely used) algorithms for analyzing proteomics data, and (3) that it is robust against random and systematic noise. We further demonstrate the applicability of our algorithm to two previously published clinical data-sets.