Nonlocal techniques for the analysis of deep ReLU neural network approximations

Recently, Daubechies, DeVore, Foucart, Hanin, and Petrova introduced a system of piece-wise linear functions, which can be easily reproduced by artificial neural networks with the ReLU activation function and which form a Riesz basis of $L_2([0,1])$. This work was generalized by two of the authors to the multivariate setting. We show that this system serves as a Riesz basis also for Sobolev spaces $W^s([0,1]^d)$ and Barron classes ${\mathbb B}^s([0,1]^d)$ with smoothness $0<s<1$. We apply this fact to re-prove some recent results on the approximation of functions from these classes by deep neural networks. Our proof method avoids using local approximations and allows us to track also the implicit constants as well as to show that we can avoid the curse of dimension. Moreover, we also study how well one can approximate Sobolev and Barron functions by ANNs if only function values are known.

Sparse Proteomics Analysis - A compressed sensing-based approach for feature selection and classification of high-dimensional proteomics mass spectrometry data

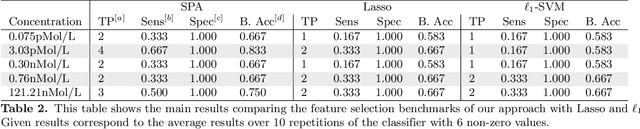
Background: High-throughput proteomics techniques, such as mass spectrometry (MS)-based approaches, produce very high-dimensional data-sets. In a clinical setting one is often interested in how mass spectra differ between patients of different classes, for example spectra from healthy patients vs. spectra from patients having a particular disease. Machine learning algorithms are needed to (a) identify these discriminating features and (b) classify unknown spectra based on this feature set. Since the acquired data is usually noisy, the algorithms should be robust against noise and outliers, while the identified feature set should be as small as possible. Results: We present a new algorithm, Sparse Proteomics Analysis (SPA), based on the theory of compressed sensing that allows us to identify a minimal discriminating set of features from mass spectrometry data-sets. We show (1) how our method performs on artificial and real-world data-sets, (2) that its performance is competitive with standard (and widely used) algorithms for analyzing proteomics data, and (3) that it is robust against random and systematic noise. We further demonstrate the applicability of our algorithm to two previously published clinical data-sets.

Learning Functions of Few Arbitrary Linear Parameters in High Dimensions

Let us assume that $f$ is a continuous function defined on the unit ball of $\mathbb R^d$, of the form $f(x) = g (A x)$, where $A$ is a $k \times d$ matrix and $g$ is a function of $k$ variables for $k \ll d$. We are given a budget $m \in \mathbb N$ of possible point evaluations $f(x_i)$, $i=1,...,m$, of $f$, which we are allowed to query in order to construct a uniform approximating function. Under certain smoothness and variation assumptions on the function $g$, and an {\it arbitrary} choice of the matrix $A$, we present in this paper 1. a sampling choice of the points $\{x_i\}$ drawn at random for each function approximation; 2. algorithms (Algorithm 1 and Algorithm 2) for computing the approximating function, whose complexity is at most polynomial in the dimension $d$ and in the number $m$ of points. Due to the arbitrariness of $A$, the choice of the sampling points will be according to suitable random distributions and our results hold with overwhelming probability. Our approach uses tools taken from the {\it compressed sensing} framework, recent Chernoff bounds for sums of positive-semidefinite matrices, and classical stability bounds for invariant subspaces of singular value decompositions.