Convergence of alternating minimisation algorithms for dictionary learning

In this paper we derive sufficient conditions for the convergence of two popular alternating minimisation algorithms for dictionary learning - the Method of Optimal Directions (MOD) and Online Dictionary Learning (ODL), which can also be thought of as approximative K-SVD. We show that given a well-behaved initialisation that is either within distance at most $1/\log(K)$ to the generating dictionary or has a special structure ensuring that each element of the initialisation only points to one generating element, both algorithms will converge with geometric convergence rate to the generating dictionary. This is done even for data models with non-uniform distributions on the supports of the sparse coefficients. These allow the appearance frequency of the dictionary elements to vary heavily and thus model real data more closely.

Dictionary learning - from local towards global and adaptive

This paper studies the convergence behaviour of dictionary learning via the Iterative Thresholding and K-residual Means (ITKrM) algorithm. On one hand it is shown that there exist stable fixed points that do not correspond to the generating dictionary, which can be characterised as very coherent. On the other hand it is proved that ITKrM is a contraction under much relaxed conditions than previously necessary. Based on the characterisation of the stable fixed points, replacing coherent atoms with carefully designed replacement candidates is proposed. In experiments on synthetic data this outperforms random or no replacement and always leads to full dictionary recovery. Finally the question how to learn dictionaries without knowledge of the correct dictionary size and sparsity level is addressed. Decoupling the replacement strategy of coherent or unused atoms into pruning and adding, and slowly carefully increasing the sparsity level, leads to an adaptive version of ITKrM. In several experiments this adaptive dictionary learning algorithm is shown to recover a generating dictionary from randomly initialised dictionaries of various sizes on synthetic data and to learn meaningful dictionaries on image data.

Compressed Dictionary Learning

In this paper we show that the computational complexity of the Iterative Thresholding and K-Residual-Means (ITKrM) algorithm for dictionary learning can be significantly reduced by using dimensionality reduction techniques based on the Johnson-Lindenstrauss Lemma. We introduce the Iterative Compressed-Thresholding and K-Means (IcTKM) algorithm for fast dictionary learning and study its convergence properties. We show that IcTKM can locally recover a generating dictionary with low computational complexity up to a target error $\tilde{\varepsilon}$ by compressing $d$-dimensional training data into $m < d$ dimensions, where $m$ is proportional to $\log d$ and inversely proportional to the distortion level $\delta$ incurred by compressing the data. Increasing the distortion level $\delta$ reduces the computational complexity of IcTKM at the cost of an increased recovery error and reduced admissible sparsity level for the training data. For generating dictionaries comprised of $K$ atoms, we show that IcTKM can stably recover the dictionary with distortion levels up to the order $\delta \leq O(1/\sqrt{\log K})$. The compression effectively shatters the data dimension bottleneck in the computational cost of the ITKrM algorithm. For training data with sparsity levels $S \leq O(K^{2/3})$, ITKrM can locally recover the dictionary with a computational cost that scales as $O(d K \log(\tilde{\varepsilon}^{-1}))$ per training signal. We show that for these same sparsity levels the computational cost can be brought down to $O(\log^5 (d) K \log(\tilde{\varepsilon}^{-1}))$ with IcTKM, a significant reduction when high-dimensional data is considered. Our theoretical results are complemented with numerical simulations which demonstrate that IcTKM is a powerful, low-cost algorithm for learning dictionaries from high-dimensional data sets.

Online and Stable Learning of Analysis Operators

In this paper four iterative algorithms for learning analysis operators are presented. They are built upon the same optimisation principle underlying both Analysis K-SVD and Analysis SimCO. The Forward and Sequential Analysis Operator Learning (FAOL and SAOL) algorithms are based on projected gradient descent with optimally chosen step size. The Implicit AOL (IAOL) algorithm is inspired by the implicit Euler scheme for solving ordinary differential equations and does not require to choose a step size. The fourth algorithm, Singular Value AOL (SVAOL), uses a similar strategy as Analysis K-SVD while avoiding its high computational cost. All algorithms are proven to decrease or preserve the target function in each step and a characterisation of their stationary points is provided. Further they are tested on synthetic and image data, compared to Analysis SimCO and found to give better recovery rates and faster decay of the objective function respectively. In a final denoising experiment the presented algorithms are again shown to perform similar to or better than the state-of-the-art algorithm ASimCO.

Dictionary Learning from Incomplete Data

This paper extends the recently proposed and theoretically justified iterative thresholding and $K$ residual means algorithm ITKrM to learning dicionaries from incomplete/masked training data (ITKrMM). It further adapts the algorithm to the presence of a low rank component in the data and provides a strategy for recovering this low rank component again from incomplete data. Several synthetic experiments show the advantages of incorporating information about the corruption into the algorithm. Finally, image inpainting is considered as application example, which demonstrates the superior performance of ITKrMM in terms of speed at similar or better reconstruction quality compared to its closest dictionary learning counterpart.

Convergence radius and sample complexity of ITKM algorithms for dictionary learning

In this work we show that iterative thresholding and K-means (ITKM) algorithms can recover a generating dictionary with K atoms from noisy $S$ sparse signals up to an error $\tilde \varepsilon$ as long as the initialisation is within a convergence radius, that is up to a $\log K$ factor inversely proportional to the dynamic range of the signals, and the sample size is proportional to $K \log K \tilde \varepsilon^{-2}$. The results are valid for arbitrary target errors if the sparsity level is of the order of the square root of the signal dimension $d$ and for target errors down to $K^{-\ell}$ if $S$ scales as $S \leq d/(\ell \log K)$.

Local Identification of Overcomplete Dictionaries

This paper presents the first theoretical results showing that stable identification of overcomplete $\mu$-coherent dictionaries $\Phi \in \mathbb{R}^{d\times K}$ is locally possible from training signals with sparsity levels $S$ up to the order $O(\mu^{-2})$ and signal to noise ratios up to $O(\sqrt{d})$. In particular the dictionary is recoverable as the local maximum of a new maximisation criterion that generalises the K-means criterion. For this maximisation criterion results for asymptotic exact recovery for sparsity levels up to $O(\mu^{-1})$ and stable recovery for sparsity levels up to $O(\mu^{-2})$ as well as signal to noise ratios up to $O(\sqrt{d})$ are provided. These asymptotic results translate to finite sample size recovery results with high probability as long as the sample size $N$ scales as $O(K^3dS \tilde \varepsilon^{-2})$, where the recovery precision $\tilde \varepsilon$ can go down to the asymptotically achievable precision. Further, to actually find the local maxima of the new criterion, a very simple Iterative Thresholding and K (signed) Means algorithm (ITKM), which has complexity $O(dKN)$ in each iteration, is presented and its local efficiency is demonstrated in several experiments.

Learning Functions of Few Arbitrary Linear Parameters in High Dimensions

Let us assume that $f$ is a continuous function defined on the unit ball of $\mathbb R^d$, of the form $f(x) = g (A x)$, where $A$ is a $k \times d$ matrix and $g$ is a function of $k$ variables for $k \ll d$. We are given a budget $m \in \mathbb N$ of possible point evaluations $f(x_i)$, $i=1,...,m$, of $f$, which we are allowed to query in order to construct a uniform approximating function. Under certain smoothness and variation assumptions on the function $g$, and an {\it arbitrary} choice of the matrix $A$, we present in this paper 1. a sampling choice of the points $\{x_i\}$ drawn at random for each function approximation; 2. algorithms (Algorithm 1 and Algorithm 2) for computing the approximating function, whose complexity is at most polynomial in the dimension $d$ and in the number $m$ of points. Due to the arbitrariness of $A$, the choice of the sampling points will be according to suitable random distributions and our results hold with overwhelming probability. Our approach uses tools taken from the {\it compressed sensing} framework, recent Chernoff bounds for sums of positive-semidefinite matrices, and classical stability bounds for invariant subspaces of singular value decompositions.

Classification via Incoherent Subspaces

This article presents a new classification framework that can extract individual features per class. The scheme is based on a model of incoherent subspaces, each one associated to one class, and a model on how the elements in a class are represented in this subspace. After the theoretical analysis an alternate projection algorithm to find such a collection is developed. The classification performance and speed of the proposed method is tested on the AR and YaleB databases and compared to that of Fisher's LDA and a recent approach based on on $\ell_1$ minimisation. Finally connections of the presented scheme to already existing work are discussed and possible ways of extensions are pointed out.

Dictionary Identification - Sparse Matrix-Factorisation via $\ell_1$-Minimisation

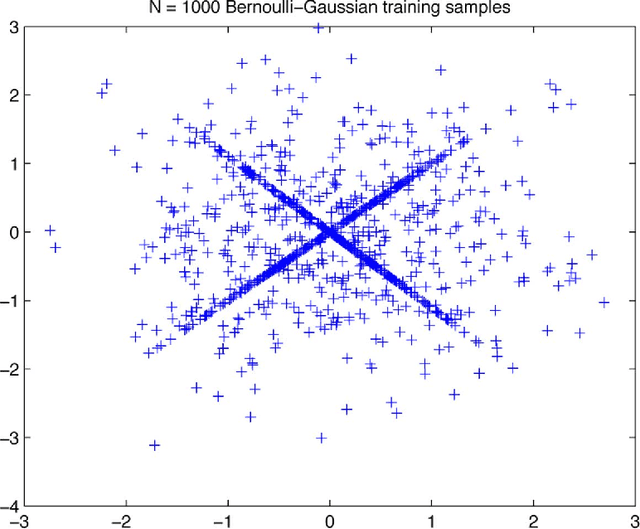
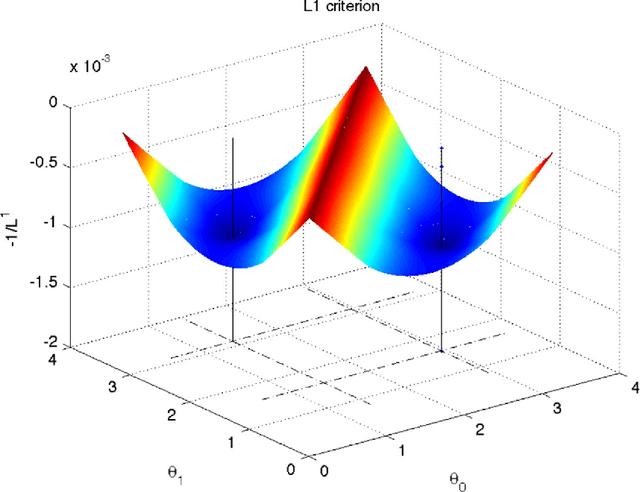
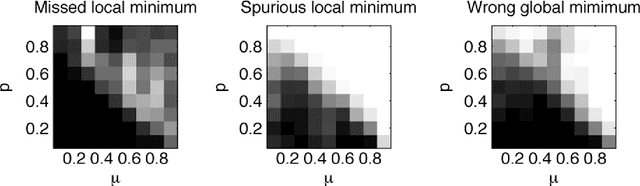
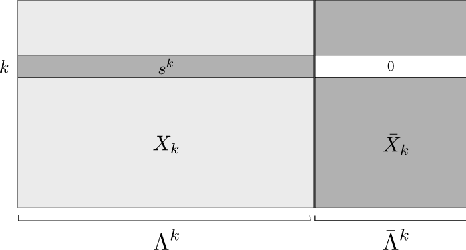
This article treats the problem of learning a dictionary providing sparse representations for a given signal class, via $\ell_1$-minimisation. The problem can also be seen as factorising a $\ddim \times \nsig$ matrix $Y=(y_1 >... y_\nsig), y_n\in \R^\ddim$ of training signals into a $\ddim \times \natoms$ dictionary matrix $\dico$ and a $\natoms \times \nsig$ coefficient matrix $\X=(x_1... x_\nsig), x_n \in \R^\natoms$, which is sparse. The exact question studied here is when a dictionary coefficient pair $(\dico,\X)$ can be recovered as local minimum of a (nonconvex) $\ell_1$-criterion with input $Y=\dico \X$. First, for general dictionaries and coefficient matrices, algebraic conditions ensuring local identifiability are derived, which are then specialised to the case when the dictionary is a basis. Finally, assuming a random Bernoulli-Gaussian sparse model on the coefficient matrix, it is shown that sufficiently incoherent bases are locally identifiable with high probability. The perhaps surprising result is that the typically sufficient number of training samples $\nsig$ grows up to a logarithmic factor only linearly with the signal dimension, i.e. $\nsig \approx C \natoms \log \natoms$, in contrast to previous approaches requiring combinatorially many samples.