Data-driven modelling of nonlinear dynamics by polytope projections and memory

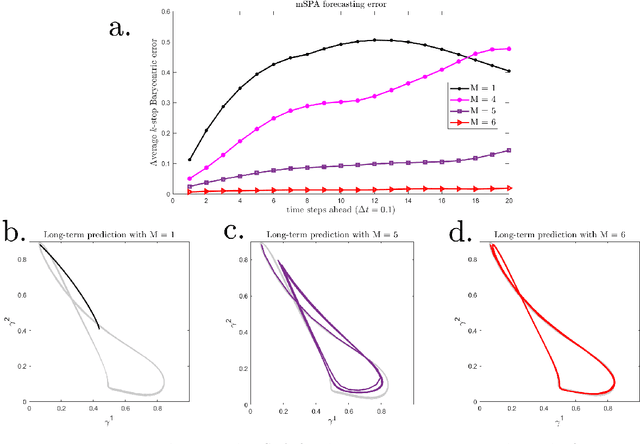
We present a numerical method to model dynamical systems from data. We use the recently introduced method Scalable Probabilistic Approximation (SPA) to project points from a Euclidean space to convex polytopes and represent these projected states of a system in new, lower-dimensional coordinates denoting their position in the polytope. We then introduce a specific nonlinear transformation to construct a model of the dynamics in the polytope and to transform back into the original state space. To overcome the potential loss of information from the projection to a lower-dimensional polytope, we use memory in the sense of the delay-embedding theorem of Takens. By construction, our method produces stable models. We illustrate the capacity of the method to reproduce even chaotic dynamics and attractors with multiple connected components on various examples.

Nonparametric approximation of conditional expectation operators

Given the joint distribution of two random variables $X,Y$ on some second countable locally compact Hausdorff space, we investigate the statistical approximation of the $L^2$-operator defined by $[Pf](x) := \mathbb{E}[ f(Y) \mid X = x ]$ under minimal assumptions. By modifying its domain, we prove that $P$ can be arbitrarily well approximated in operator norm by Hilbert--Schmidt operators acting on a reproducing kernel Hilbert space. This fact allows to estimate $P$ uniformly by finite-rank operators over a dense subspace even when $P$ is not compact. In terms of modes of convergence, we thereby obtain the superiority of kernel-based techniques over classically used parametric projection approaches such as Galerkin methods. This also provides a novel perspective on which limiting object the nonparametric estimate of $P$ converges to. As an application, we show that these results are particularly important for a large family of spectral analysis techniques for Markov transition operators. Our investigation also gives a new asymptotic perspective on the so-called kernel conditional mean embedding, which is the theoretical foundation of a wide variety of techniques in kernel-based nonparametric inference.

Kernel autocovariance operators of stationary processes: Estimation and convergence

We consider autocovariance operators of a stationary stochastic process on a Polish space that is embedded into a reproducing kernel Hilbert space. We investigate how empirical estimates of these operators converge along realizations of the process under various conditions. In particular, we examine ergodic and strongly mixing processes and prove several asymptotic results as well as finite sample error bounds with a detailed analysis for the Gaussian kernel. We provide applications of our theory in terms of consistency results for kernel PCA with dependent data and the conditional mean embedding of transition probabilities. Finally, we use our approach to examine the nonparametric estimation of Markov transition operators and highlight how our theory can give a consistency analysis for a large family of spectral analysis methods including kernel-based dynamic mode decomposition.