Philipp-Immanuel Schneider
Review and experimental benchmarking of machine learning algorithms for efficient optimization of cold atom experiments
Dec 20, 2023Abstract:The generation of cold atom clouds is a complex process which involves the optimization of noisy data in high dimensional parameter spaces. Optimization can be challenging both in and especially outside of the lab due to lack of time, expertise, or access for lengthy manual optimization. In recent years, it was demonstrated that machine learning offers a solution since it can optimize high dimensional problems quickly, without knowledge of the experiment itself. In this paper we present results showing the benchmarking of nine different optimization techniques and implementations, alongside their ability to optimize a Rubidium (Rb) cold atom experiment. The investigations are performed on a 3D $^{87}$Rb molasses with 10 and 18 adjustable parameters, respectively, where the atom number obtained by absorption imaging was chosen as the test problem. We further compare the best performing optimizers under different effective noise conditions by reducing the Signal-to-Noise ratio of the images via adapting the atomic vapor pressure in the 2D+ MOT and the detection laser frequency stability.
Impact Study of Numerical Discretization Accuracy on Parameter Reconstructions and Model Parameter Distributions
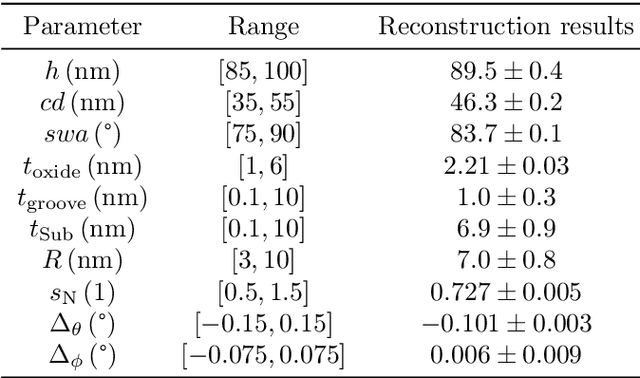
May 04, 2023Abstract:Numerical models are used widely for parameter reconstructions in the field of optical nano metrology. To obtain geometrical parameters of a nano structured line grating, we fit a finite element numerical model to an experimental data set by using the Bayesian target vector optimization method. Gaussian process surrogate models are trained during the reconstruction. Afterwards, we employ a Markov chain Monte Carlo sampler on the surrogate models to determine the full model parameter distribution for the reconstructed model parameters. The choice of numerical discretization parameters, like the polynomial order of the finite element ansatz functions, impacts the numerical discretization error of the forward model. In this study we investigate the impact of numerical discretization parameters of the forward problem on the reconstructed parameters as well as on the model parameter distributions. We show that such a convergence study allows to determine numerical parameters which allow for efficient and accurate reconstruction results.
Bayesian Target-Vector Optimization for Efficient Parameter Reconstruction
Feb 23, 2022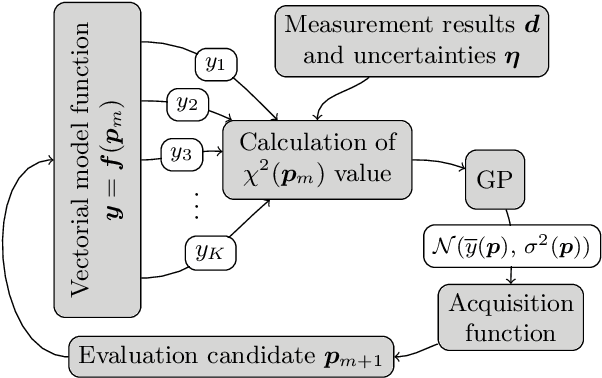
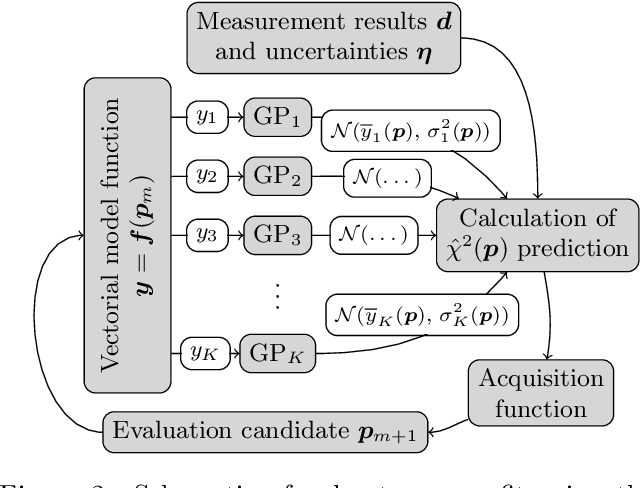
Abstract:Parameter reconstructions are indispensable in metrology. Here, on wants to explain $K$ experimental measurements by fitting to them a parameterized model of the measurement process. The model parameters are regularly determined by least-square methods, i.e., by minimizing the sum of the squared residuals between the $K$ model predictions and the $K$ experimental observations, $\chi^2$. The model functions often involve computationally demanding numerical simulations. Bayesian optimization methods are specifically suited for minimizing expensive model functions. However, in contrast to least-square methods such as the Levenberg-Marquardt algorithm, they only take the value of $\chi^2$ into account, and neglect the $K$ individual model outputs. We introduce a Bayesian target-vector optimization scheme that considers all $K$ contributions of the model function and that is specifically suited for parameter reconstruction problems which are often based on hundreds of observations. Its performance is compared to established methods for an optical metrology reconstruction problem and two synthetic least-squares problems. The proposed method outperforms established optimization methods. It also enables to determine accurate uncertainty estimates with very few observations of the actual model function by using Markov chain Monte Carlo sampling on a trained surrogate model.
Recent advances in Bayesian optimization with applications to parameter reconstruction in optical nano-metrology
Jul 12, 2021



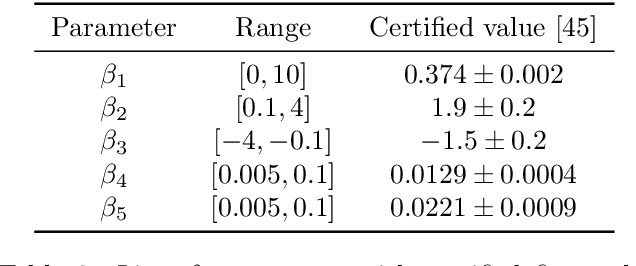
Abstract:Parameter reconstruction is a common problem in optical nano metrology. It generally involves a set of measurements, to which one attempts to fit a numerical model of the measurement process. The model evaluation typically involves to solve Maxwell's equations and is thus time consuming. This makes the reconstruction computationally demanding. Several methods exist for fitting the model to the measurements. On the one hand, Bayesian optimization methods for expensive black-box optimization enable an efficient reconstruction by training a machine learning model of the squared sum of deviations. On the other hand, curve fitting algorithms, such as the Levenberg-Marquardt method, take the deviations between all model outputs and corresponding measurement values into account which enables a fast local convergence. In this paper we present a Bayesian Target Vector Optimization scheme which combines these two approaches. We compare the performance of the presented method against a standard Levenberg-Marquardt-like algorithm, a conventional Bayesian optimization scheme, and the L-BFGS-B and Nelder-Mead simplex algorithms. As a stand-in for problems from nano metrology, we employ a non-linear least-square problem from the NIST Standard Reference Database. We find that the presented method generally uses fewer calls of the model function than any of the competing schemes to achieve similar reconstruction performance.
* Proceedings article, SPIE conference "Modeling Aspects in Optical Metrology VIII"
Bayesian optimization with improved scalability and derivative information for efficient design of nanophotonic structures
Jan 08, 2021



Abstract:We propose the combination of forward shape derivatives and the use of an iterative inversion scheme for Bayesian optimization to find optimal designs of nanophotonic devices. This approach widens the range of applicability of Bayesian optmization to situations where a larger number of iterations is required and where derivative information is available. This was previously impractical because the computational efforts required to identify the next evaluation point in the parameter space became much larger than the actual evaluation of the objective function. We demonstrate an implementation of the method by optimizing a waveguide edge coupler.
Using Gaussian process regression for efficient parameter reconstruction
Mar 28, 2019Abstract:Optical scatterometry is a method to measure the size and shape of periodic micro- or nanostructures on surfaces. For this purpose the geometry parameters of the structures are obtained by reproducing experimental measurement results through numerical simulations. We compare the performance of Bayesian optimization to different local minimization algorithms for this numerical optimization problem. Bayesian optimization uses Gaussian-process regression to find promising parameter values. We examine how pre-computed simulation results can be used to train the Gaussian process and to accelerate the optimization.
* 8 pages, 4 figures
Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction
Sep 18, 2018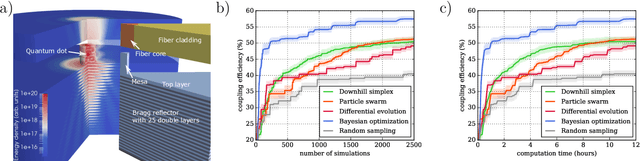
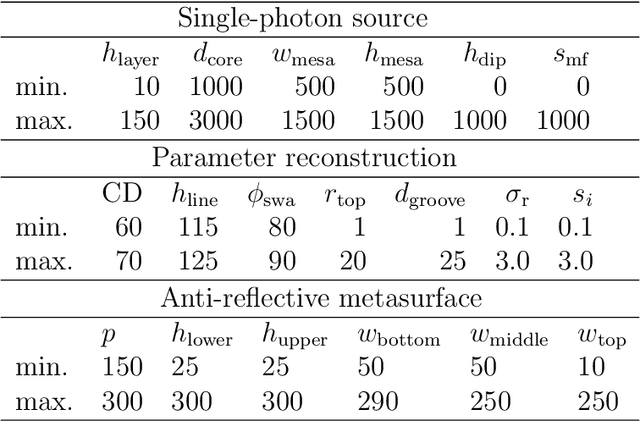
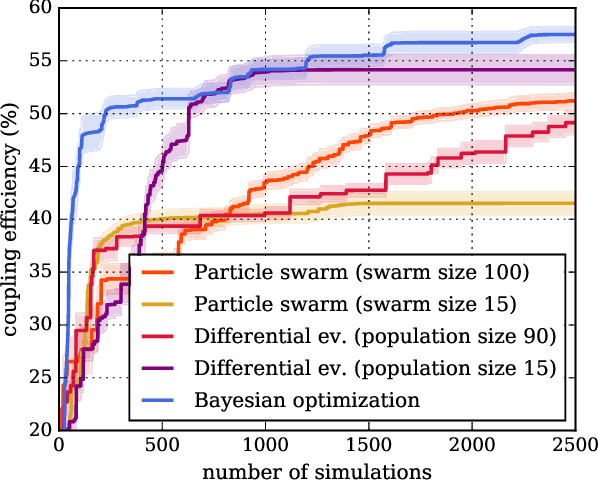
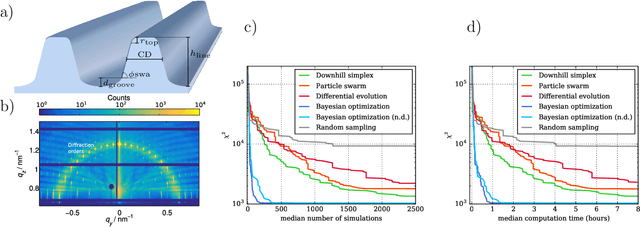
Abstract:Numerical optimization is an important tool in the field of computational physics in general and in nano-optics in specific. It has attracted attention with the increase in complexity of structures that can be realized with nowadays nano-fabrication technologies for which a rational design is no longer feasible. Also, numerical resources are available to enable the computational photonic material design and to identify structures that meet predefined optical properties for specific applications. However, the optimization objective function is in general non-convex and its computation remains resource demanding such that the right choice for the optimization method is crucial to obtain excellent results. Here, we benchmark five global optimization methods for three typical nano-optical optimization problems from the field of shape optimization and parameter reconstruction: downhill simplex optimization, the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm, particle swarm optimization, differential evolution, and Bayesian optimization. In these examples, Bayesian optimization, mainly known from machine learning applications, obtains significantly better results in a fraction of the run times of the other optimization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge