Anna Andrle
Bayesian Target-Vector Optimization for Efficient Parameter Reconstruction
Feb 23, 2022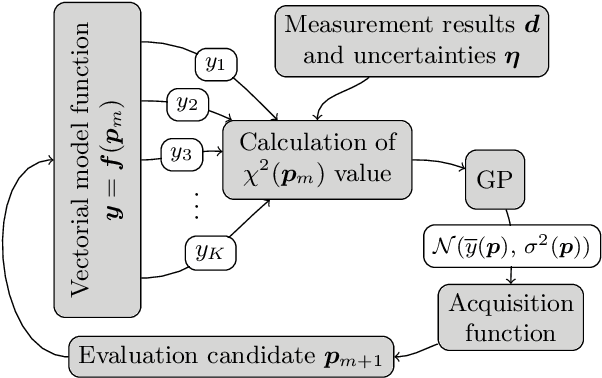
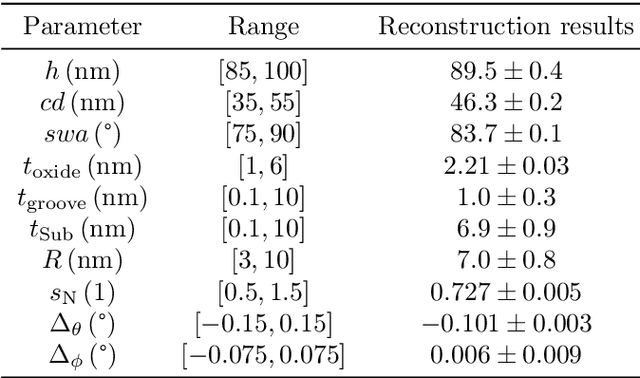
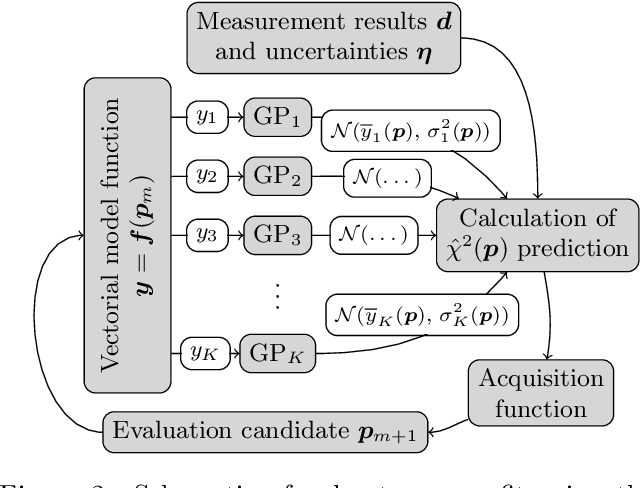
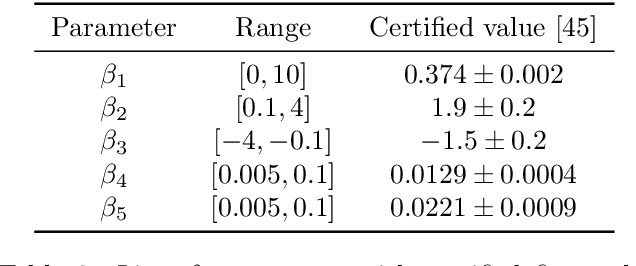
Abstract:Parameter reconstructions are indispensable in metrology. Here, on wants to explain $K$ experimental measurements by fitting to them a parameterized model of the measurement process. The model parameters are regularly determined by least-square methods, i.e., by minimizing the sum of the squared residuals between the $K$ model predictions and the $K$ experimental observations, $\chi^2$. The model functions often involve computationally demanding numerical simulations. Bayesian optimization methods are specifically suited for minimizing expensive model functions. However, in contrast to least-square methods such as the Levenberg-Marquardt algorithm, they only take the value of $\chi^2$ into account, and neglect the $K$ individual model outputs. We introduce a Bayesian target-vector optimization scheme that considers all $K$ contributions of the model function and that is specifically suited for parameter reconstruction problems which are often based on hundreds of observations. Its performance is compared to established methods for an optical metrology reconstruction problem and two synthetic least-squares problems. The proposed method outperforms established optimization methods. It also enables to determine accurate uncertainty estimates with very few observations of the actual model function by using Markov chain Monte Carlo sampling on a trained surrogate model.
Invertible Neural Networks versus MCMC for Posterior Reconstruction in Grazing Incidence X-Ray Fluorescence
Feb 05, 2021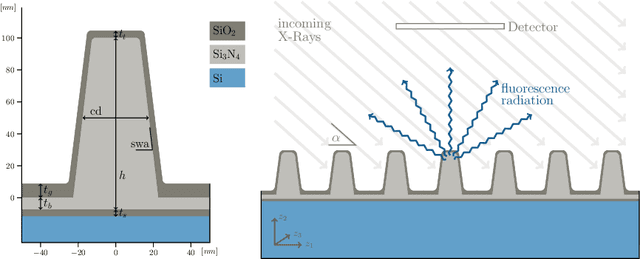
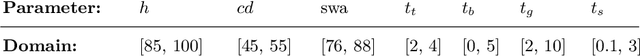
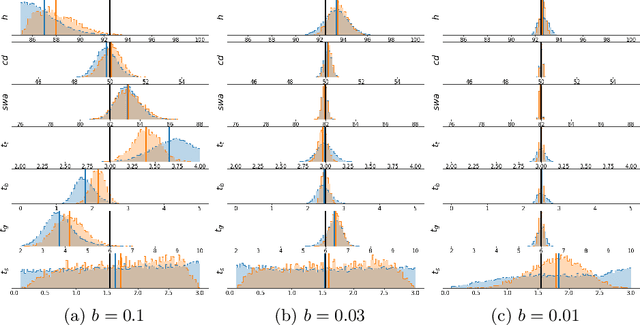
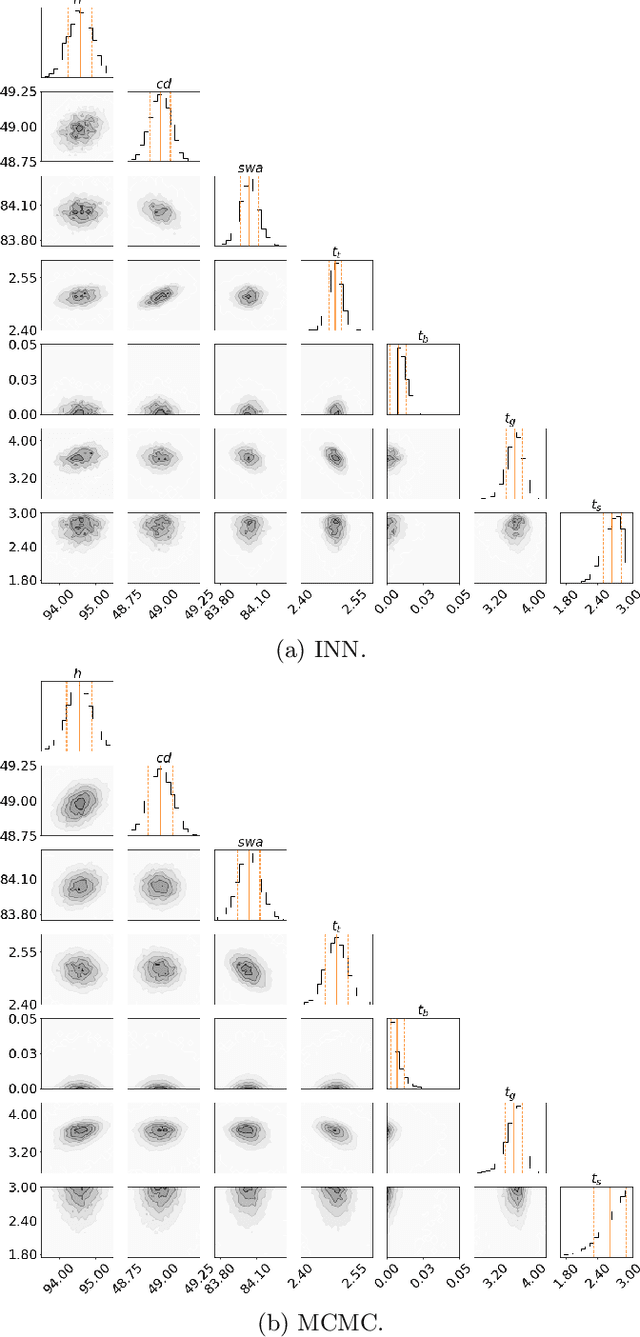
Abstract:Grazing incidence X-ray fluorescence is a non-destructive technique for analyzing the geometry and compositional parameters of nanostructures appearing e.g. in computer chips. In this paper, we propose to reconstruct the posterior parameter distribution given a noisy measurement generated by the forward model by an appropriately learned invertible neural network. This network resembles the transport map from a reference distribution to the posterior. We demonstrate by numerical comparisons that our method can compete with established Markov Chain Monte Carlo approaches, while being more efficient and flexible in applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge