Impact Study of Numerical Discretization Accuracy on Parameter Reconstructions and Model Parameter Distributions

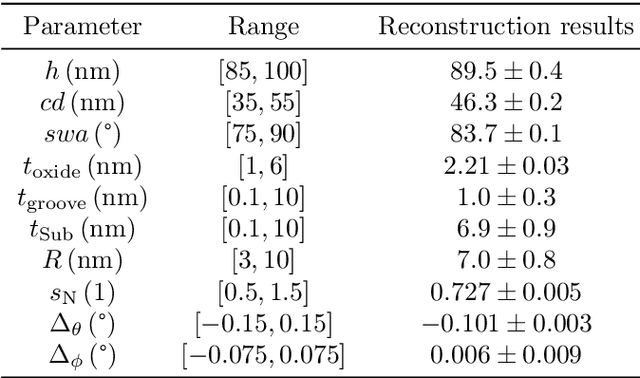
Numerical models are used widely for parameter reconstructions in the field of optical nano metrology. To obtain geometrical parameters of a nano structured line grating, we fit a finite element numerical model to an experimental data set by using the Bayesian target vector optimization method. Gaussian process surrogate models are trained during the reconstruction. Afterwards, we employ a Markov chain Monte Carlo sampler on the surrogate models to determine the full model parameter distribution for the reconstructed model parameters. The choice of numerical discretization parameters, like the polynomial order of the finite element ansatz functions, impacts the numerical discretization error of the forward model. In this study we investigate the impact of numerical discretization parameters of the forward problem on the reconstructed parameters as well as on the model parameter distributions. We show that such a convergence study allows to determine numerical parameters which allow for efficient and accurate reconstruction results.

Bayesian Target-Vector Optimization for Efficient Parameter Reconstruction

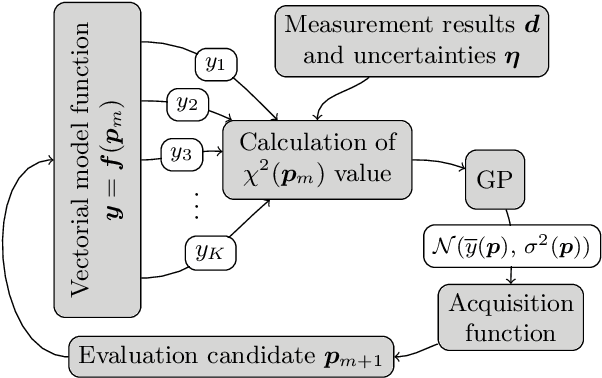
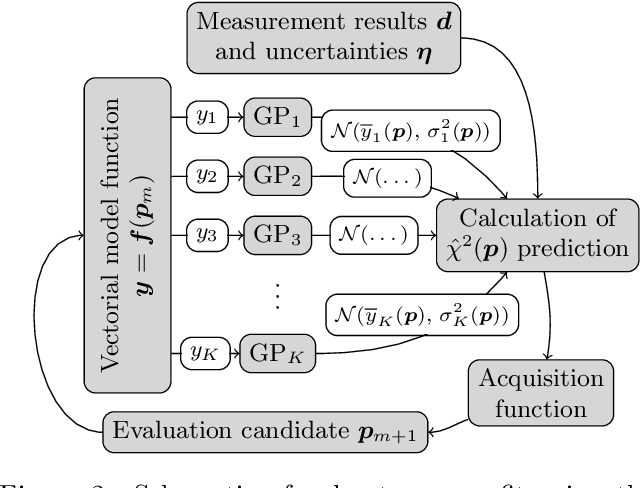
Parameter reconstructions are indispensable in metrology. Here, on wants to explain $K$ experimental measurements by fitting to them a parameterized model of the measurement process. The model parameters are regularly determined by least-square methods, i.e., by minimizing the sum of the squared residuals between the $K$ model predictions and the $K$ experimental observations, $\chi^2$. The model functions often involve computationally demanding numerical simulations. Bayesian optimization methods are specifically suited for minimizing expensive model functions. However, in contrast to least-square methods such as the Levenberg-Marquardt algorithm, they only take the value of $\chi^2$ into account, and neglect the $K$ individual model outputs. We introduce a Bayesian target-vector optimization scheme that considers all $K$ contributions of the model function and that is specifically suited for parameter reconstruction problems which are often based on hundreds of observations. Its performance is compared to established methods for an optical metrology reconstruction problem and two synthetic least-squares problems. The proposed method outperforms established optimization methods. It also enables to determine accurate uncertainty estimates with very few observations of the actual model function by using Markov chain Monte Carlo sampling on a trained surrogate model.

Recent advances in Bayesian optimization with applications to parameter reconstruction in optical nano-metrology

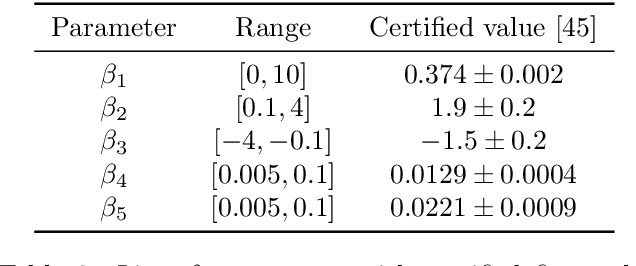
Parameter reconstruction is a common problem in optical nano metrology. It generally involves a set of measurements, to which one attempts to fit a numerical model of the measurement process. The model evaluation typically involves to solve Maxwell's equations and is thus time consuming. This makes the reconstruction computationally demanding. Several methods exist for fitting the model to the measurements. On the one hand, Bayesian optimization methods for expensive black-box optimization enable an efficient reconstruction by training a machine learning model of the squared sum of deviations. On the other hand, curve fitting algorithms, such as the Levenberg-Marquardt method, take the deviations between all model outputs and corresponding measurement values into account which enables a fast local convergence. In this paper we present a Bayesian Target Vector Optimization scheme which combines these two approaches. We compare the performance of the presented method against a standard Levenberg-Marquardt-like algorithm, a conventional Bayesian optimization scheme, and the L-BFGS-B and Nelder-Mead simplex algorithms. As a stand-in for problems from nano metrology, we employ a non-linear least-square problem from the NIST Standard Reference Database. We find that the presented method generally uses fewer calls of the model function than any of the competing schemes to achieve similar reconstruction performance.